$\gdef\d{\mathrm{d}}\gdef\sgn{\operatorname{sgn}}\gdef\e{\mathrm{e}}\gdef\bm#1{\boldsymbol{#1}}$
这些内容主要写于 2024 年上半年我自学高中物理时想到的一些问题。实际上是 2025.2.23 upload 这个文章的,现在看起来很幼稚了,就只是当作记录吧。
小球上半圆弧模型
众所周知,上到一半是 $\sqrt{2gr}$,从顶上飞出去是 $\sqrt{5gr}$。那斜抛刚好落到圆弧与水平面连接处呢?
设斜抛起始点与圆心连线与水平夹角为 $\theta$,高度为 $h$。 $$ \left\{\begin{align*} h&=r(1+\sin\theta)\\ \dfrac 12mv_0^2&=\dfrac 12mv^2+mgh\\ m\dfrac{v^2}r&=mg\sin\theta\\ h&=\dfrac 12gt^2-vt\cos\theta\\ r\cos\theta&=vt\sin\theta \end{align*}\right. $$ 解得 $\sin\theta=\frac 12,v_0=\sqrt{3.5gr}$。
恒定功率加速问题
考虑机车从静止开始以恒定功率 $P$ 加速,阻力为 $f$,希望求出 $v$ 关于 $t$ 的表达式。根据牛二, $$ \frac Pv-f=m\dot v $$ 即 $$ \dfrac{mv}{P-fv}\d v=\d t $$
两边积分然后根据 $v|_{t=0}=0$ 即可解得 $C$。
当 $f=0$ 时,解得 $$ v=\sqrt{\frac{2Pt}m} $$ 其余情况下有 $$ \frac mf\left(\frac Pf\ln\frac P{P-fv}-v\right)=t $$ 当 $t\to+\infin$ 时 $v\to P/f$。$v$ 关于 $t$ 不存在初等表达式,需借助 Lambert W 函数。
如果阻力正比于 $v$ 即 $f(v)=kv$,则 $$ v=\sqrt{\frac{P(1-\e^{-\frac{2k}mt})}k} $$
真正的自由落体运动
method from zby(的同学).
视星体为质量为 $M$ 的质点,记 $y$ 为轻物体(如果是两个星体,以其中一个为参考系即可)距质点的距离。初始 $y|_{t=0}=d$,速度为 $0$。
然后会得到这样一个微分方程: $$ \ddot yy=GM $$ 不会解……
换一个思路,由能量守恒, $$ -{GM}d=-{GM}y+\frac12{\dot y}^2 $$ 即 $$ \dot y=\sqrt{2GM\left(\frac 1y-\frac 1d\right)} $$ 那就是(我们来详细推导一下) $$ \begin{align*} t={}&\int_{y}^d\frac{\d x}{\sqrt{2GM\left(\frac 1x-\frac 1d\right)}}\\ \xlongequal{z=\sqrt{\frac 1x-\frac 1d}}{}&\sqrt{\frac{2}{GM}}\int_{0}^{\sqrt{\frac 1y-\frac 1d}}\frac{\d z}{\left(z^2+\frac 1d\right)^2}\\ \xlongequal{\tan\alpha=\sqrt dz}{}&\sqrt{\frac{2d^3}{GM}}\int_0^{\arctan\sqrt{\frac dy-1}}\cos^2\alpha\d\alpha\\ ={}&\sqrt{\frac{2d^3}{GM}}\left.\left(\frac{\sin2\alpha}{4}+\frac\alpha2\right)\right|_0^{\arctan\sqrt{\frac dy-1}}\\ ={}&\sqrt{\frac{d}{2GM}}\left(y\sqrt{\frac dy-1}+d\arctan\sqrt{\frac dy-1}\right) \end{align*} $$ 因此,相撞时刻为 $$ t|_{y\to 0}=\frac\pi2d\sqrt\frac d{2GM} $$
开普勒推万有引力
开普勒第一定律
所有行星绕恒星运动的轨道都是椭圆,且恒星处在椭圆的某个焦点上。
以 $F_1$ 为极点,$F_1F_2$ 为极轴建立极坐标系,行星轨迹为
$$ r=\frac{ep}{1-e\cos\theta} $$
开普勒第二定律
一对特定恒星与行星的连线在相等时间内所扫过的面积相等。
设 $S$ 为单位时间内扫过的面积,则 $$ 2S=r^2\dot\theta $$
开普勒第三定律
对于一个恒星,其所有行星轨道半长轴的立方与公转周期的平方成正比。
设该比例为 $k$,即 $$ \frac{a^3}{T^2}=k $$ 又 $$ T\cdot S=\pi ab $$ 故 $$ S^2=\frac{\pi^2kb^2}{a} $$
极坐标下的加速度
将极坐标下的加速度正交分解成径向加速度 $a_r$ 与切向加速度 $a_\theta$。
极坐标下有径向基矢 $\hat r=\hat x\cos\theta+\hat y\sin\theta$ 和 切向基矢 $\hat\theta=-\hat x\sin\theta+\hat y\cos\theta$。
首先有 $$ \begin{align*} \d\hat r&=\hat\theta\d\theta\\ \d\hat\theta&=-\hat r\d r \end{align*} $$ 故 $$ \begin{align*} \frac{\d(r\hat r)}{\d t}&=\dot r\hat r+r\hat\theta\\ \frac{\d^2(r\hat r)}{\d t^2}&=\left(\ddot r-r\dot\theta^2\right)\hat r+\left(2\dot r\dot\theta+r\ddot\theta\right)\hat\theta\\ \end{align*} $$ 即 $$ \begin{align*} a_r&=\ddot r-r\dot\theta^2\\ a_\theta&=2\dot r\dot\theta+r\ddot\theta \end{align*} $$
推导
综合上述公式, $$ \begin{align*} \dot r&=-\frac{e^2p\sin\theta}{(1-e\cos\theta)^2}\dot\theta\\ &=-\frac{r^2\dot\theta}{p}\sin\theta\\ &=-\frac{2S}{p}\sin\theta\\ \ddot r&=-\frac{2S}{p}\dot\theta\cos\theta\\ &=-\frac{2S}{p}\left(\frac 1e-\frac pr\right)\dot\theta\\ a_r&=\ddot r-r\dot\theta^2\\ &=-\frac{2S}{ep}\dot\theta+\frac{2S}{r}\dot\theta-\frac{2S}{r}\dot\theta\\ &=-\frac{2S}{ep}\cdot\frac{2S}{r^2}\\ &=-\frac{4\pi^2kb^2}{aepr^2}\\ &=-\frac{4\pi^2k}{r^2}\\ a_\theta&=2\dot r\dot\theta+r\ddot\theta\\ &=\frac{\d(r^2\theta)}{r\d t}\\ &=0 \end{align*} $$ 由牛二,引力方向为两星球连线,大小为 $$ F=\frac{4\pi^2km}{r^2} $$ 设恒星与行星质量分别为 $m_1,m_2$,对应常数分别为 $k_1,k_2$,由牛三, $$ \frac{4\pi^2k_1m_2}{r^2}=\frac{4\pi^2k_2m_1}{r^2} $$ 即 $$ \frac{k_1}{m_1}=\frac{k_2}{m_2} $$ 由此可见,存在一常数,所有物体的 $k$ 比 $m$ 均为该常数,设其为 $\frac{G}{4\pi^2}$,则 $$ F=\frac{Gm_1m_2}{r^2} $$
非质点的库仑力计算
对于一个半径为 $R$,均匀带电 $Q$ 的圆环,与圆心连线垂直于圆面且长为 $D$ 的点处的电场大小为(相似三角形分解力) $$ \frac{kQD}{(R^2+D^2)^{\frac 32}} $$ 对于一个半径为 $R$,均匀带电 $Q$ 的球壳,与球心距离为 $D$ 处的电场大小为 $$ \begin{align*} &\int_{-\frac\pi 2}^{\frac\pi 2}\frac{k\left(\frac{2\pi R^2\cos\theta\d\theta}{4\pi R^2}Q\right)(D-R\sin\theta)}{\left[R^2\cos^2\theta+(D-R\sin\theta)^2\right]^{\frac 32}}\\ ={}&\frac{kQ}{2}\int_{-\frac\pi 2}^{\frac\pi 2}\frac{\cos\theta\d\theta(D-R\sin\theta)}{\left(R^2+D^2-2RD\sin\theta\right)^{\frac 32}}\\ ={}&\frac{kQ}{2}\left.\frac{D\sin\theta-R}{D^2\sqrt{R^2+D^2-2RD\sin\theta}}\right|_{-\frac\pi 2}^{\frac\pi 2}\\ ={}&\frac{kQ}{2D^2}(1+\sgn(D-R)) \end{align*} $$ 于是一个半径为 $R$,均匀带电 $Q$ 的实心球,与球心距离为 $D$ 处的电场大小为 $$ \left\{\begin{align*} &\dfrac{kQD}{R^3},&D<R\\ &\dfrac{kQ}{D^2},&D\ge R \end{align*}\right. $$ 因此均匀带电的球对于某点的电场,等效于去除在该点外围的球的部分后,球心对其的电场。
对于一个半径为 $R$,均匀带电 $Q$ 的圆板,与圆心连线垂直于圆面且长为 $D$ 的点处的电场大小为 $$ \begin{align*} &\int_0^R\frac{k\left(\frac{2\pi r\d r}{\pi R^2}Q\right)D}{\left(r^2+D^2\right)^{\frac 32}}\\ ={}&\frac{2kQD}{R^2}\int_0^R\frac{r\d r}{(r^2+D^2)^{\frac 32}}\\ ={}&\frac{2kQD}{R^2}\left(\left.-\frac{1}{\sqrt{R^2+D^2}}\right|_0^R\right)\\ ={}&\frac{2kQ}{R^2}\left(1-\frac{D}{\sqrt{R^2+D^2}}\right) \end{align*} $$ $R\to+\infty$ 可导出电荷面密度为 $\sigma$ 的无限大均匀带电平面的电场大小为 $2\pi k\sigma$(与距离无关),同时可以导出电容的决定式 $$ C=\frac QU=\frac Q{Ed}=\frac Q{2\cdot 2\pi k\sigma\cdot d}=\frac S{4\pi kd} $$ 对于一个电荷线密度为 $\lambda$ 的无限长均匀带电导线,与它距离为 $D$ 处的电场大小为 $$ \int_{-\infty}^{\infty}\frac{k(\lambda\d x)D}{(x^2+D^2)^{\frac 32}}=\frac{2k\lambda}{D} $$
对于一个半径为 $R$,均匀带电,电荷线密度为 $\lambda$ 的圆环,在圆所在平面内,与圆心距离为 $D$ 处的电场大小为 $$ \int_0^{2\pi}\frac{k(R\d\theta\cdot\lambda)(D-R\sin\theta)}{(R^2+D^2-2RD\sin\theta)^{\frac32}} $$ 然后这个玩意 TM 积不出来!是个椭圆积分。反而下面这个是可以积的:
对于一个半径为 $R$,均匀带电,电荷面密度为 $\sigma$ 的无限长圆筒,与轴心距离为 $D$ 处的电场大小为 $$ \int_0^{2\pi}\frac{2k(R\d\theta\cdot\sigma)(D-R\sin\theta)}{R^2+D^2-2RD\sin\theta}=\frac{2\pi k\sigma R}D(1+\sgn(D-R)) $$ 于是一个半径为 $R$,均匀带电,电荷体密度为 $\rho$ 的无限长圆柱,与轴心距离为 $D$ 处的电场大小为 $$ \left\{\begin{align*} &2\pi k\rho D,&D<R\\ &\dfrac{2\pi k\rho R^2}{D},&D\ge R \end{align*}\right. $$ 因此均匀带电的圆柱对于某点的电场,等效于去除在该点外围的圆柱的部分后,轴心对其的电场。
通电导线的磁场
直导线的磁场分布和带电导线的电场分布是类似的,都是与距离成反比,只是方向不同。
对于一个半径为 $R$,电流为 $I$ 的圆导线,与圆心距离为 $D$ 处的磁感应强度大小为 $$ \int_0^{2\pi}这部分咕了 $$
通电螺线管的磁场
对于一个半径为 $R$,面电流密度为 $\sigma$($\sigma$ 在数值上等于 $nI$,$n$ 为单位宽度上的匝数。电流为逆时针方向)的无限长通电螺线管,与轴心距离为 $D$ 处的磁感应强度大小为:
假设螺线管轴心与 $z$ 轴重合,现拿出一段宽为 $\d l$,与 $z$ 轴平行的无限长条,设它的电流方向为 $(d_x,d_y,0)$(模长为 $1$)。若将它平移到 $z$ 轴处,它对 $(x,y,0)$ 处的磁感应强度为 $$ \begin{align*} &\d l\int_{-\infty}^{+\infty}\frac{k\sigma\d z\cdot(d_x,d_y,0)\times(x,y,-z)}{\left(x^2+y^2+z^2\right)^{\frac32}}\\ ={}&k\sigma\d l\cdot(d_x,d_y,0)\times\left(\frac{2x}{x^2+y^2},\frac{2y}{x^2+y^2},0\right)\\ ={}&2k\sigma\d l\frac{d_xy-d_yx}{x^2+y^2}\cdot\vec k \end{align*} $$ 回到原问题 $$ \int_0^{2\pi}2k\sigma R\d\theta\frac{-\sin\theta(D-R\sin\theta)-\cos\theta(-R\cos\theta)}{R^2+D^2-2RD\sin\theta}=2\pi k\sigma(1-\sgn(D-R)) $$ 因此理想的通电螺线管,管内为强度为 $\mu_0\sigma$ 的匀强磁场,管上的强度为管内的一半,管外无磁场。
电容充放电过程
充电过程中,设电源电压为 $E$,电容电压为 $U$,整个电路的电阻为 $R$。 $$ C\dot U=\dot Q=I=\frac{E-U}{R} $$ 解得 $$ U=E(1-\e^{-\frac t{CR}}) $$ 同理可得到放电过程(这里的 $E$ 指电容的初始电压) $$ U=E\e^{-\frac t{CR}} $$ 无论哪种情况,都有 $$ I=\frac{\e^{-\frac t{CR}}}{R} $$
碰撞问题的理解
关于非弹性碰撞时的能量损耗,可以理解为两者相对于质心的速度的减小,详见这个回答。在这个回答中提到说,一个系统的动能等于其质心动能加上各部分相对于质心的动能,这是一个有趣的结论: $$ \sum m_i\bm{v_i}^2=M\bm{V}^2+\sum m_i(\bm{v_i}-\bm{V})^2\\ \text{which }M=\sum m_i,\bm{V}=\sum\bm{v_i} $$ 直接展开即证。
关于完全非弹性碰撞必定共速的原因,可以从两个角度理解。
第一个角度就是直接求最值: $$ \max;\frac12m_1v_1^2+\frac12m_2v_2^2-\frac12m_1{v_1’}^2-\frac12m_2{v_2’}^2\\ \text{s.t.};m_1v_1+m_2v_2=m_1v_1’+m_2v_2’ $$ 建立一个坐标系,横轴是 $\sqrt{m_1}v_1$,纵轴是 $\sqrt{m_2}v_2$。那么所有合法的情况都处于一条斜率为 $-\sqrt{m_1/m_2}$ 的直线上。完全非弹性碰撞就是其上与原点距离最近的点,也就是原点到该直线的垂足,而这条垂线的斜率为 $\sqrt{m_2/m_1}$,其上面的点就是 $v_1=v_2$。弹性碰撞可以视作关于这条垂线对称。
第二个角度就是假想两球之间连了一个轻弹簧。那么弹簧长度最小或最大时,两球相对静止,这时弹簧的弹性势能最大,动能减少量最大。
对了,考虑求一下弹簧的长度关于时间的函数?设伸长量为 $x$,初始为 $0$。 $$ \left\{\begin{align*} \dot{v_1}&=\frac{kx}{m_1}\\ \dot{v_2}&=-\frac{kx}{m_2}\\ \dot{x}&=v_2-v_1 \end{align*}\right.\Rightarrow \ddot{x}=-k\left(\frac1{m_1}+\frac1{m_2}\right)x $$ 解得 $x=\dfrac{v\sin\sqrt cx}{\sqrt c}$,其中 $c=k\left(\dfrac1{m_1}+\dfrac1{m_2}\right)$,$v$ 为初始的相对速度。
因此这时实际上做的是类似简谐运动。同时可以轻松求出能量损耗最大值为 $$ \frac 12kx_{\max}^2=\frac{m_1m_2v^2}{2(m_1+m_2)} $$
单摆相关
考察一个初始时轻绳与竖直方向夹角为 $\theta_0$ 且初速度为 $0$ 的摆的周期。
夹角到 $\theta$ 时,速度满足 $$ \frac12mv^2=mgl(\cos\theta-\cos\theta_0) $$ 故周期为 $$ \begin{align*} T(\theta_0)={}&4\int_0^{\theta_0}\frac{l\d\theta}{\sqrt{2gl(\cos\theta-\cos\theta_0)}}\\ ={}&2\sqrt{\frac lg}\int_0^{\theta_0}\frac{\d\theta}{\sqrt{\sin^2\frac{\theta_0}{2}-\sin^2\frac{\theta}{2}}}\\ \xlongequal{\sin\alpha=\frac{\sin\frac{\theta}{2}}{\sin\frac{\theta_0}{2}}}{}&4\sqrt{\frac lg}\int_0^{\frac\pi2}\frac{\d\alpha}{\sqrt{1-\sin^2\frac{\theta_0}{2}\sin^2\alpha}}\\ ={}&4\sqrt{\frac lg}\cdot K\left(\sin\frac{\theta_0}{2}\right) \end{align*} $$ 其中 $K(a)$ 为第一类完全椭圆积分。推导中最难的一步是换元,我也是从知乎上看来的(几篇都是这么搞的)。
从而也可以验证书中的公式 $\lim_{\theta_0\to 0}T(\theta_0)=2\pi\sqrt{l/g}$。另外 $T(\pi/2)\approx 7.4163\sqrt{l/g}$。
如果换成轻杆也是一样的。对于能绕一整周的情况,设在顶部时速度为 $v_0$,那么周期为 $$ 2\int_0^\pi\frac{l\d\theta}{\sqrt{2gl(1+\cos\theta)+v_0^2}}=\frac{4l}{\sqrt{4gl+v_0^2}}K\left(\sqrt\frac{4gl}{4gl+v_0^2}\right) $$
可以将上面的两种情况统一一下。如果能量等效高度为 $h$,令 $r=h/2l$, $$ T’(r)=\left\{\begin{align*}&2\sqrt{\dfrac lg}K\left(\sqrt r\right),\quad&r<1\\ &2\sqrt{\dfrac l{gr}}K\left(\frac 1{\sqrt r}\right),\quad&r>1\end{align*}\right. $$ 为了整齐起见,$r<1$ 时 $T’(r)$ 表示半周期。
悬链线
设曲线的函数为 $y=f(x)$,其中最低点在 $y$ 轴上,两头在 $(\pm d,0)$。
首先,由于悬空部分只受重力作用,故绳每一点的张力横向分力均相等,设为 $T$。则点 $x$ 处的张力纵向分力大小为 $T\cdot\lvert f’(x)\rvert$。
取绳上小段 $x$ 到 $x+\d x$,由受力平衡, $$ T(f’(x+\d x)-f’(x))=\rho g\sqrt{1+f’(x)^2}\d x $$ 即 $$ y’’=\frac{\rho g}T\sqrt{1+{y’}^2} $$ 记 $k=\rho g/T$,解得 $$ y=\frac{\cosh kx-\cosh kd}{k} $$ 其中 $T$ 一般由绳长 $l$ 确定,满足 $$ l=\frac{2\sinh kd}{k} $$
机械振动
简谐振动
简谐振动满足方程 $$ \ddot x=-\frac kmx $$ 有通解 $$ x=A\sin(\omega t+\varphi) $$ 其中 $A,\omega,\varphi$ 可以由系统已知量和初始情况 $x_0,v_0$ 确定(记 $\alpha=k/m$): $$ \begin{align*} \omega&=\sqrt\alpha\\ A&=\sqrt{x_0^2+\frac{v_0^2}\alpha}\\ \varphi&=\mathrm{atan2}\left(x_0,\frac{v_0}{\sqrt\alpha}\right) \end{align*} $$
阻尼振动
阻尼振动满足方程(阻力正比于速度) $$ \ddot x=-\alpha x-\beta\dot x $$ 根据微分方程相关理论,要讨论 $\Delta=\beta^2-4\alpha$ 的正负。
临界阻尼
当 $\Delta=0$ 时 $$ x=\e^{-\frac\beta2t}\left(x_0+\frac\beta2x_0t+v_0t\right) $$
临界阻尼是收敛最快的。
过阻尼
当 $\Delta>0$ 时 $$ x=\e^{-\frac\beta2t}\left(x_0\cosh\frac{\sqrt\Delta}2t+\frac{\beta x_0+2v_0}{\sqrt\Delta}\sinh\frac{\sqrt\Delta}2t\right) $$
欠阻尼
当 $\Delta<0$ 时 $$ x=\e^{-\frac\beta2t}A\sin(\omega t+\varphi) $$ 其中 $$ \begin{align*} \omega&=\frac{\sqrt{-\Delta}}2\\ A&=\sqrt{x_0^2-\frac{(\beta x_0+2v_0)^2}\Delta}\\ \varphi&=\mathrm{atan2}\left(\frac{x_0}A,\frac{\beta x_0+2v_0}{\sqrt{-\Delta}A}\right) \end{align*} $$ 由此可知欠阻尼振动的周期为 $$ T=\frac{4\pi}{\sqrt{4\alpha-\beta^2}} $$
对比图
令 $\alpha=1,x_0=1,v_0=0$。
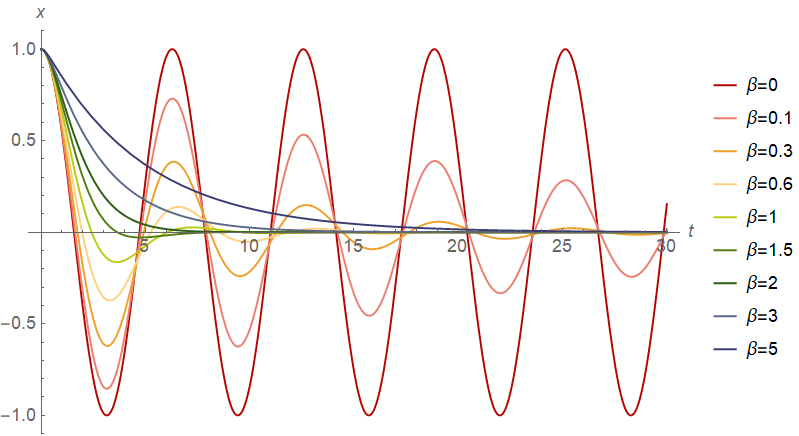
(有没有人能告诉我 Mathematica 里 Plot Legended 的图例的线长怎么改啊)
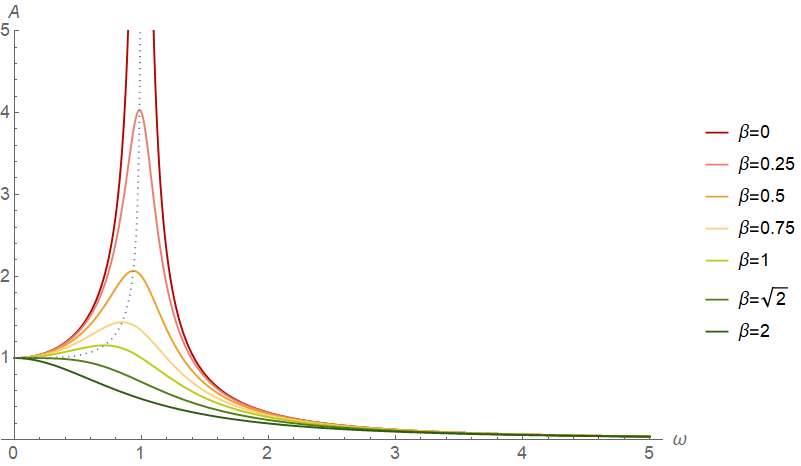
受迫振动
受迫振动满足方程 $$ \ddot x=-\alpha x-\beta\dot x+\gamma\cos\omega t $$ 解微分方程过程中,可以发现它能被拆分成无策动力的阻尼振动和频率为策动力频率的简谐振动。
对于 $\beta\ne 0$ 的情况,前者趋近于 $0$,后者振幅为(完整表达式这里就不算了) $$ A=\frac\gamma{\sqrt{(\alpha-\omega^2)^2+(\beta\omega)^2}} $$ 如果 $\beta^2<2\alpha$,则取到最大值时 $$ \omega=\sqrt{\alpha-\frac{\beta^2}2},A=\frac\gamma{\beta\sqrt{\alpha-\dfrac{\beta^2}4}} $$ 否则 $\omega\to 0$ 时,$A\to A_{\max}=\gamma/\alpha$。
对于 $\beta=0$ 的情况,假设初始 $x|_{t=0}=\dot x|_{t=0}=0$。如果 $\omega^2\ne \alpha$,则 $$ x=\frac\gamma{\alpha-\omega^2}\left(\cos\omega t-\cos\sqrt\alpha t\right) $$ 在 $\omega/\sqrt\alpha\in\R\setminus\mathbb{Q}$ 时,$\sup\lvert x\rvert=2\gamma/\lvert\alpha-\omega^2\rvert$,其余情况下 $x_{\max}$ 或 $x_{\min}$ 会很难求。实际分析时,我们会认为 $\beta$ 较小但不为 $0$,这样 $A\approx\gamma/\lvert\alpha-\omega^2\rvert$。
如果 $\omega^2=\alpha$,则 $$ x=\frac{\gamma t\sin\omega t}{2\omega} $$ 综上,$A$ 的公式可以推广到任意 $\alpha,\omega>0,\beta\ge 0$。
对比图
令 $\alpha=\gamma=1$。蓝色虚线表示最优顶点。由此可见,当 $\beta\ll\alpha$ 时,$\omega=\sqrt\alpha$ 会导致共振。
粒子在磁场中的运动轨迹
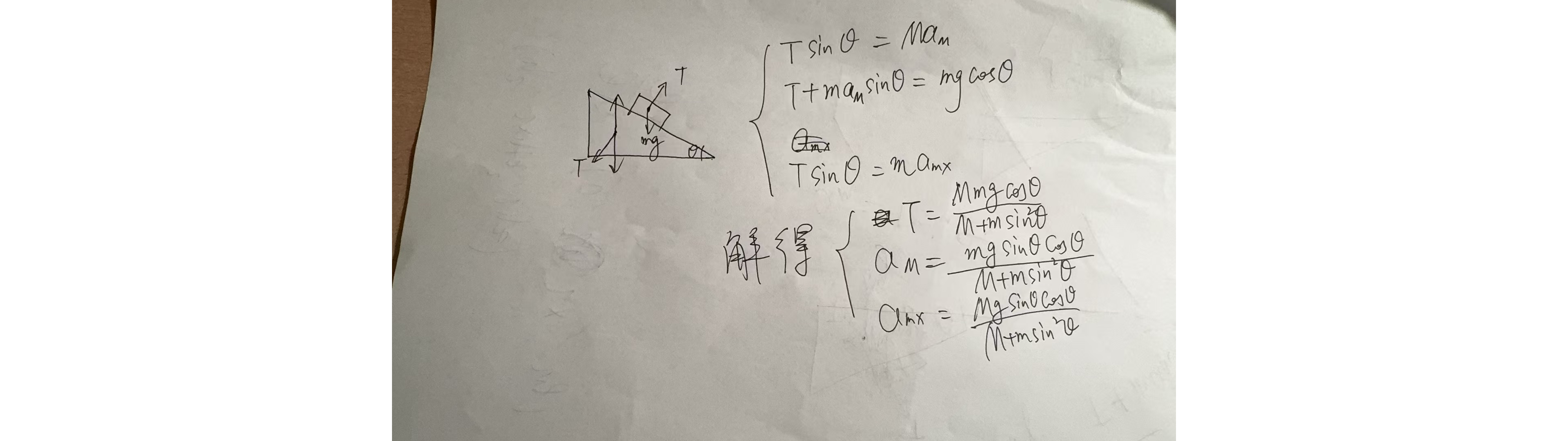
一个质量为 $m$,电荷量为 $+q$ 的带电粒子在磁感应强度为 $B$ 的匀强磁场中静止释放,考虑重力。取垂直于磁场的面作平面直角坐标系,磁场向内,原点为初始位置,向右为 $x$ 轴正方向,向下为 $y$ 轴正方向。 $$ \left\{\begin{align*} qB\dot y&=m\ddot x\\ -qB\dot x+mg&=m\ddot y \end{align*}\right. $$ 令 $k=qB/m$。两式分别求导代入另一式,结合初始条件解得 $$ \left\{\begin{align*} x&=\frac g{k^2}(kt-\sin kt)\\ y&=\frac g{k^2}(1-\cos kt) \end{align*}\right. $$ 这是摆线。
章动
以陀螺脚为参考点。考虑质心在圆盘中心,设质量为 $m$,质心为 $\vec{l}$,转动惯量为 $I$,角动量为 $\vec{L}$。
陀螺在一个瞬间的运动可以用两个量描述:自转的角速度 $\omega$,公转的速度 $\vec{v}$。 $$ \left\{\begin{align*} \vec{l}\cdot\vec{v}&=\vec{0}\\ m\vec{l}\times\vec{v}+I\omega\cdot\frac{\vec{l}}{\lvert\vec{l}\rvert}&=\vec{L} \end{align*}\right. $$ 解得 $$ \left\{\begin{align*} \omega&=\frac{\vec{L}\cdot\vec{l}}{I\lvert\vec{l}\rvert}\\ m\vec{l}\times\vec{v}&=\vec{L}-\frac{\vec{L}\cdot\vec{l}}{\vec{l}\cdot\vec{l}}\cdot\vec{l} \end{align*}\right. $$ 另有 $$ \dot{\vec{L}}=\vec{l}\times\vec{G} $$ 不会解。猜想:$\vec{l}$ 是关于时间的三角函数。