这里主要讲一下 Nash-Williams 定理的证明。
一张图 $G$ 的边集能划分成 $k$ 个森林 $\Leftrightarrow$ 其每个非空导出子图的 $\lvert E\rvert\le k(\lvert V\rvert-1)$。允许重边。
$\Rightarrow$ 显然,$\Leftarrow$ 的证明:
以下称一个非空导出子图“合法”为 $\lvert E\rvert\le k(\lvert V\rvert-1)$,“满”为 $\lvert E\rvert=k(\lvert V\rvert-1)$。记 $G[S]$ 为 $G$ 中节点子集 $S$ 的导出子图。
证 1($k=2$,P5295/UOJ#168 题解里的证法):归纳。现考虑度数最小的点 $u$,由鸽巢,其度数至多为 $3$。其余情况平凡,度数为 $3$ 时,设相连点为 $v_{1\sim 3}$,这时删去 $u$,待证的即为在这三个点间加某条边,可以划分,这样加回 $u$ 时只需在这条额外边中间放上 $u$ 即可。
如果不行,也就是说分别存在包含 $v_1$ 与 $v_2$、包含 $v_1$ 与 $v_3$、包含 $v_2$ 与 $v_3$ 的三个满的导出子图(它们不能额外加边)由于 $G_1+G_2=G_1\cup G_2+G_1\cap G_2$,故两个有公共点的满子图,它们的交、并均为满。故存在一个包含 $v_1$、$v_2$ 与 $v_3$ 的满子图,那么包括进 $u$ 时,这个子图就不合法了,矛盾。
这个思路在 $k\ge 2$ 时需要稍加修改才能沿用。
证 2(论文):考虑度数最小的点 $u$,由鸽巢,其度数 $d\le 2k-1$,且 $d\le k$ 时平凡。设 $u$ 邻边的另一个端点从小到大依次为 $v_{1\sim d}$(可重),现在考虑以下过程:对 $i=1\sim d-k$,时刻 $i$ 时将 $e_i=(u,v_i)$ 去掉,加入 $e^\prime_i=(v_i,v_{i+k})$(显然 $v_i\ne v_{i+k}$)。记 $G^\prime$ 为改完的图。
如果直到操作完都没有不合法,那就令 $S=V\setminus\set u$,$t=d-k$。否则假设时刻 $t+1$ 是第一个出现不合法的时刻,那么时刻 $t$ 可以找到一个不含 $u$ 的满子图 $G^\prime[S]$,不妨设 $t$ 及之前所有连上新边的点都在 $S$ 内。在时刻 $t$ 后中止上述过程。
先归纳构造 $G^\prime[S]$ 的拆分方案,然后将 $S$ 缩成一个点,这时得到的图 $G^{\prime\prime}$ 的导出子图也均合法,第一种情况显然,第二种情况,如果找到了一个不合法的子图,那和 $G^\prime[S]$ 并在一起也不合法,矛盾。因此也构造出 $G^{\prime\prime}$ 的方案。对于 $G^\prime[S]$ 方案中的一个森林,如果有某个 $e^\prime_i$ 属于它,那么将它与 $G^{\prime\prime}[S]$ 中包含 $e_{i+k}$ 的那个并起来(有多个 $i$ 则任选),称这样得到的为第一类;对于其他森林,随意配对并起来,为第二类。显然目前并出的各图均为森林。
现在类似于前面的思路,要把 $e^\prime_i$ 还原回中间接了个 $u$ 的原图方案,即在各个第一类森林中删 $e^\prime_i$ 加回 $e_i$。这样可能导致环,即 $u$ 原来就与 $v_i$ 通过 $e_i^\prime$ 以外的边连通,且删了 $e^\prime_i$ 后 $v_{i+k}$ 与 $u$ 不连通了(不然原来会有环)。找到包含 $e_{i+k}$ 的森林,它一定是第二类,这是因为归纳构造时 $S$ 被缩起来了,故 $e_{i+k}$ 不会与其他 $e_{j+k}$($j\le t$)处于同一个森林中。把这两个森林里的 $e_{i}$ 与 $e_{i+k}$ 互换即可。这不会在这个第二类森林中引入环,也是因为构造时 $S$ 被缩起来,即 $u$ 与 $S$ 内 $v$ 间的边对连通性的影响是无区分的,而第二类森林两端在 $S$ 内的边又不会变动(如果不区分一二类森林,直接随便配对并,就可能在还原时无法避免环)。
然后还有一个对边归纳的思路。
证 3(论文):任取一条边 $(u,v)$,归纳构造不含它的方案,这时如果在某个森林中 $u$、$v$ 不连通,则直接补进去即可;否则考虑某个森林 $G_1$ 中它们所在的连通块,设点集为 $S$。在其余森林中分别取出 $S$ 的导出子图,至少有一个导出子图不连通(否则加回 $(u,v)$ 时就不合法了),找出它对应的原森林 $G_2$。
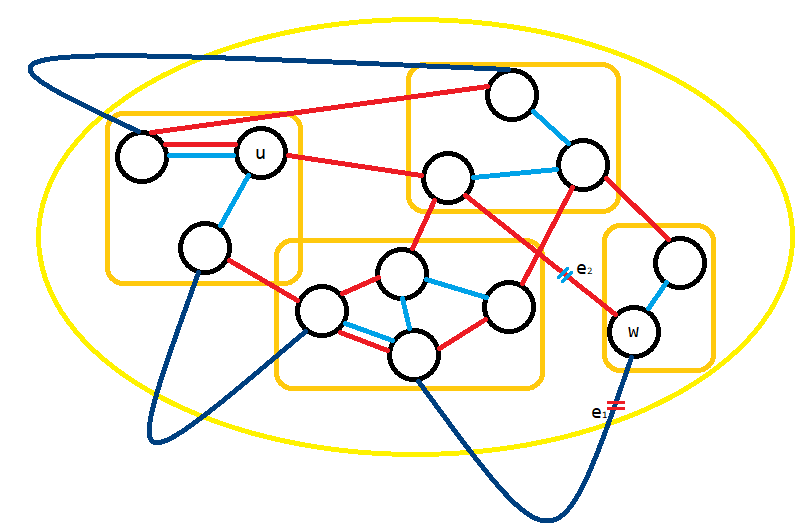
如果考虑进 $G_2$ 的所有边时,$S$ 中的点仍不连通,那么可从 $G_1[S]$ 中取出一条边改放到 $G_2$ 中使 $G_2$ 仍为森林(与图拟阵的证明相同);否则,若将 $G_2[S]$ 中各连通块缩成点,那么这些点在 $G_2$ 中的位置关系形成类似树的结构,至少有两个叶子。这说的意思是,$G_2[S]$ 中存在至少两个连通块,如果断开其与 $S$ 之外的某条边,它就与其他 $G_2[S]$ 的连通块都不连通了。选出非 $u$ 所在的这样一个连通块,设其点集为 $S^\prime$,它与其他连通块连接的唯一“向外通道”为边 $e_1$,$e_1$ 在 $S$ 中侧端点为 $w$,考虑 $G_1$ 中 $u\rightsquigarrow w$ 路径上第一条一端在 $S^\prime$ 内的边 $e_2$。将 $e_1$ 换到 $G_1$,$e_2$ 换到 $G_2$,这样两图仍为森林,且 $G_1$ 中 $u$ 所在连通块变小。如此进行下去,直到 $G_1$ 中 $u$、$v$ 不连通即可。
下图为最后一种情况,红色边为 $G_1$,蓝色与深蓝色边为 $G_2$,深蓝色边省略了在 $S$ 以外的中转点。实质上最后一种情况就是费尽心思想强制让 $G_1[S]$ 丢掉一些点,同时在丢掉点时 $u$ 所在部分不能和别的连通块连起来。
要判断一个图是否满足上述条件,问题就变为最大权闭合子图问题:选边为 $+1$,选点为 $-k$,要求结果 $\le -k$。为了避免空图,可以强制选一条边(增流)或一个点(退流)。
对于 CF1951I,有另一个性质是,所有满足条件的连边情况构成一个拟阵,交换性的证明是,对于两张图的森林划分,考虑边数多的图边数最多的森林与边数少的图的边数最少的森林,套用图拟阵的证明方式即可。边不能一条条地加,考虑二分下一次加边失败的边权,失败后这条边就可以忽略了。时间复杂度 $\mathrm{O}(m^5\log mW)$。(这题用退流似乎没什么优势?)