$\gdef\ker{\mathop{\mathrm{Ker}}}\gdef\im{\mathop{\mathrm{Im}}}\gdef\e{\mathrm{e}}\gdef\d{\mathrm{d}}\gdef\F{\mathbb{F}}\gdef\r{\operatorname{rank}}\gdef\L{\mathsf{L}}\gdef\mat#1{\begin{bmatrix}#1\end{bmatrix}}\gdef\dat#1{\begin{vmatrix}#1\end{vmatrix}}\gdef\T{\mathsf{T}}\gdef\U{\mathsf{U}}\gdef\E{\mathsf{E}}$
前言
完全从线性变换角度去讲线性代数，主要就是六个递进的难点：秩—零化度定理、行列秩相等、Cayley–Hamilton 定理、对偶、内积空间下的对偶、正交相关定理。反而行列式、SVD、Jordan 之类的没有那么难理解，只是麻烦罢了。
线性变换最难解释的是转置，转置没有一个直观的意义，例如转置的行列式等于原行列式这种东西。无论是否在内积空间下，转置只能用范畴论去理解，画出对偶的交换图，它其实也是很自然的，但再往后，到了复正规矩阵和实对称矩阵可以正规对角化这里，就完全不懂了，只能背证明。
但总的来说我线性代数没记特别多东西，Cayley–Hamilton 定理和对偶相关的理解就咕掉了。
题
只使用线性变换的知识（不使用初等行变换）证明 $\dim\ker f+\dim\im f=\dim V$。
$\ker f$ 是 $V$ 的一个子空间。取出它的一组基 $\set{v_{1\sim n}}$，并将它扩展成 $V$ 的基 $\set{v_{1\sim n},v_{n+1\sim m}}$。现在 $f(v_{1\sim n})=0$，而我们要证的是，$\set{f(v_{n+1\sim m})}$ 线性无关，从而它是 $\im f$ 的基。 $$ \sum c_if(v_i)=0\Longleftrightarrow f\left(\sum c_iv_i\right)=0\Longleftrightarrow \sum c_iv_i\in\ker f $$ 这里 $\sum$ 是 $\sum_{i=n+1}^m$。要么 $c$ 全都是 $0$，要么 $\set{v_{1\sim m}}$ 不是基。
只使用线性变换的知识（不使用初等行变换）证明行秩等于列秩。
考虑 $A_{n\times m}$ 的行空间的对偶空间，这个空间就是 $\F^m/\ker A$，于是 $$ 行秩=m-\dim\ker A=m-(m-\dim\im A)=列秩 $$ 这里的核心思路是说，将 $A$ 以两种方式看成同一个线性变换：一种是将 $A$ 视作某个对偶空间（对偶空间的对偶空间与原空间间存在自然映射，在这个问题里更简单，就是个点乘）——这个是行的，一种是直接考虑 $A$ 的线性变换——这个是列的。那么剩下的问题其实是证明原空间和对偶空间的维数相等，这个是用基来证的。
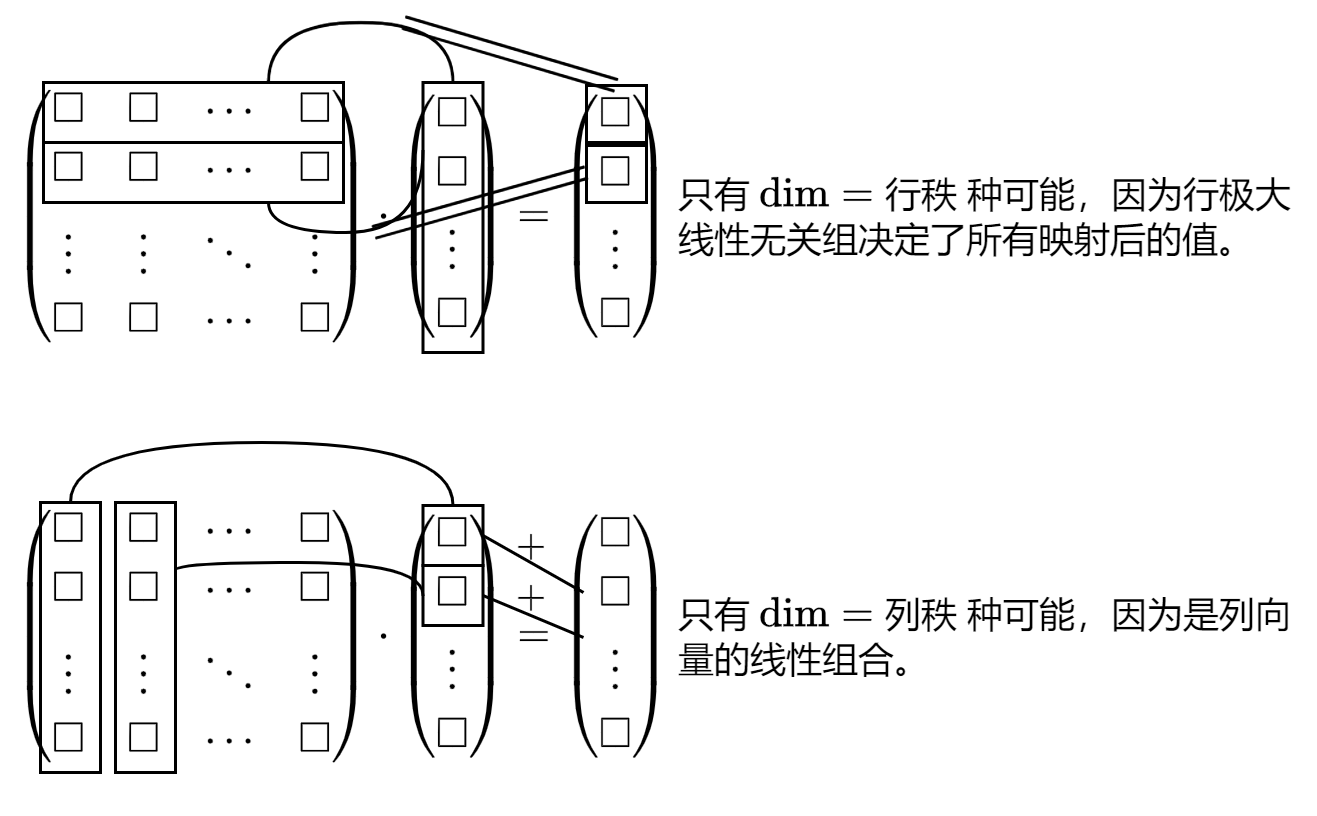
$f:V\to V$。证明 $\exists k$，$V=\ker f^k\oplus\im f^k$。
我们知道 $\im f^{k+1}\subseteq\im f^k$，于是 $\exists k$，$\dim V>\dim\im f>\dim\im f^2>\cdots>\dim\im f^k=\dim\im f^{k+1}=\dim\im f^{k+2}=\cdots$。如果 $\ker f^k\cap\im f^k\supseteq\set{0,v}$，则 $f^{2k}(v)=0$，矛盾。
这个命题在抽代里也有一个对应的版本。
$A_{n\times m}$，$B_{m\times l}$。证明 $\r(A)+\r(B)-m\le\r(AB)$。
首先，我们有，对于 $f:U\to V$，$g:V\to W$， $$ \dim\ker f+\dim\ker g\ge\dim\ker(g\circ f) $$ 直观上很好理解，证明： $$ \dim\ker(g\circ f)=\dim(\ker f\oplus\ker g|_{\im f})=\dim\ker f+\dim\ker g|_{\im f}\le\dim\ker f+\dim\ker g $$
于是 $$ \begin{align*} \r(AB)&=\dim\im\L_{AB}\\ &=\dim\im(\L_A\circ\L_B)\\ &=l-\dim\ker(\L_A\circ\L_B)\\ &\ge l-\dim\ker\L_A-\dim\ker\L_B\\ &=l-m+\dim\im\L_A-l+\dim\im\L_v\\ &=\r(A)+\r(B)-m \end{align*} $$ 可选的一种类似的思路：先证 $\dim\im(g\circ f)\ge\dim\im f-\dim\ker g$：$\dim\im f=\dim\ker g|_{\im f}+\dim\im g|_{\im f}$。
$A_{n\times n}$，$B_{n\times n}$，$AB=BA=O$，$\r(A^2)=\r(A)$。证明 $\r(A+B)=\r(A)+\r(B)$。
思路 1：证明 $\ker\L_{A+B}=\ker\L_A\cap\ker\L_B$ 与 $\ker\L_A+\ker\L_B=\R^n$。
- $(A+B)x=0\Rightarrow Ax=A(A+B)x=0$，$(A+B)x=0\Rightarrow Bx=-Ax=0\Rightarrow\ker\L_{A+B}\subseteq\ker\L_A\cap\ker\L_B$。
- $\r(A^2)=\r(A)\Rightarrow\ker\L_A\oplus\im\L_A=\R^n$，$BA=0\Rightarrow\im\L_A\subseteq\ker\L_B\Rightarrow\ker\L_A+\ker\L_B=\R^n$。
思路 2：证明 $\im\L_{A+B}=\im\L_A+\im\L_B$ 与 $\im\L_A\cap\im\L_B=\set{0}$。
- $\im\L_A=\im\L_{A^2+BA}=\im\L_{(A+B)A}\subseteq\im\L_{A+B}$；$\im\L_B=\im\L_{A+B-A}\subseteq\im\L_{A+B}+\im\L_A=\im\L_{A+B}$。
- $\r(A^2)=\r(A)\Rightarrow\ker\L_A\oplus\im\L_A=\R^n$，$AB=O\Rightarrow\im\L_B\subseteq\ker\L_A$。
$A_{m\times n}$，$B_{n\times m}$，证明 $\r(AB)=\r(A)\Rightarrow\exists C_{m\times n},A=ABC$。
设 $A=[\alpha_i]$。$Ae_i=\alpha_i$，而 $\ker\L_{AB}=\ker\L_A$ 故 $\exists\gamma_i$，$AB\gamma_i=\alpha_i$。令 $C=[\gamma_i]$。
$A_{n\times n}$。证明若 $\forall x\in\R^n$，$x\ne 0$，$|x^\top Ax|<|x^\top x|$，则 $I-A^2$ 可逆。
$|x^\top Ax|<|x^\top x|$ 展开： $$ -\sum x_i^2<\sum\sum x_ix_ja_{ij}<+\sum x_i^2\\ \Longrightarrow \left\{ \begin{aligned} x^\top(I-A)x=\sum\sum x_ix_j(\delta_{ij}-a_{ij})>0\\ x^\top(I+A)x=\sum\sum x_ix_j(\delta_{ij}+a_{ij})>0 \end{aligned} \right. $$ 如果 $I-A$ 不可逆，则 $\exists x\ne 0$，$(I-A)x=0$，那么 $x^{\top}(I-A)x=0$，矛盾。
同理 $I+A$ 可逆，于是 $I-A^2$ 可逆。
$A_{m\times n}$，$B_{n\times m}$，证明 $\r(I_m+AB)-\r(I_n+BA)=m-n$。
$$ \begin{bmatrix}I_m+AB&O\\ O&I_n\end{bmatrix}\sim\begin{bmatrix}I_m+AB&A\\ O&I_n\end{bmatrix}\sim\begin{bmatrix}I_m&A\\ -B&I_n\end{bmatrix}\sim\begin{bmatrix}I_m&A\\ O&I_n+BA\end{bmatrix}\sim\begin{bmatrix}I_m&O\\ O&I_n+BA\end{bmatrix} $$
https://zhuanlan.zhihu.com/p/473406438
TMD 为什么我记了这个期末考却没想起来？？
$A_{l\times m}$，$B_{n\times p}$，$C_{l\times p}$。证明：
- $W_{p\times n}$，$BWB=B$ 总是有解。
- $X_{m\times n}$，$AXB=C$ 有解 $\Leftrightarrow \r(A)=\r(\begin{bmatrix}A&C\end{bmatrix})\land\r\left(\begin{bmatrix}B\\ C\end{bmatrix}\right)$
设 $\r(B)=r$。通过消成相抵标准形，可以得到 $B=PQ$ 满秩分解，其中 $P_{n\times r}$ 是列满秩，$Q_{r\times p}$ 是行满秩。构造 $W=B^+=Q^\top(QQ^\top)^{-1}(P^\top P)^{-1}P^\top$。只需证明 $\r(QQ^\top)=\r(P^\top P)=r$ 即可，这个直接用一般的公式（同解证）。
$\Leftarrow$：构造 $X=A^+CB^+$。根据条件，$AY=C$、$ZB=C$ 均有解，故 $$ AXB=AA^+CB^+B=AA^+AYB^+B=AYB^+B=CB^+B=ZBB^+B=ZB=C $$
$a\in\R^n$，求 $\dat{I+aa^\top}$。
思路 1：根据行列式的拆分公式，可以把 $\dat{I+aa^\top}$ 拆成 $2^n$ 个行列式的和，其中如果有两行都取自 $aa^\top$ 就是 $0$，剩下的就是 $1+\sum a_i^2$。
思路 2：考虑 $(I+aa^\top)v=\lambda v\Leftrightarrow aa^\top v=(\lambda-1)v$。我们知道 $a\ne 0$ 时 $\dim aa^\top=1$，故有 $n-1$ 重 $\lambda-1=0$。另一重怎么考虑呢？代入 $v=a$ 得 $aa^\top v=a(a^\top v)=\braket{a,a}a$。
$$ \dat{\lambda&1&0&\cdots&0&0\\ n&\lambda&2&\cdots&0&0\\ 0&n-1&\lambda&\cdots&0&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&\cdots&\lambda&n\\ 0&0&0&\cdots&1&\lambda} $$
思路 1：令原式为 $D_n(\lambda)$。 $$ \begin{align*} D_n(\lambda)={}&\dat{\lambda&1&0&0&\cdots&0&0&0\\ n&\lambda&2&0&\cdots&0&0&0\\ 0&n-1&\lambda&3&\cdots&0&0&0\\ 0&0&n-2&\lambda&\cdots&0&0&0\\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\ 0&0&0&0&\cdots&\lambda&n-1&0\\ 0&0&0&0&\cdots&2&\lambda&n\\ 0&0&0&0&\cdots&0&1&\lambda}\\ \xlongequal{r_1\xleftarrow{+}r_2+\cdots+r_{n+1}}{}&\dat{\lambda+n&\lambda+n&\lambda+n&\lambda+n&\cdots&\lambda+n&\lambda+n&\lambda+n\\ n&\lambda&2&0&\cdots&0&0&0\\ 0&n-1&\lambda&3&\cdots&0&0&0\\ 0&0&n-2&\lambda&\cdots&0&0&0\\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\ 0&0&0&0&\cdots&\lambda&n-1&0\\ 0&0&0&0&\cdots&2&\lambda&n\\ 0&0&0&0&\cdots&0&1&\lambda}\\ \xlongequal{c_2,\cdots,c_{n+1}\xleftarrow{-}c_1}{}&\dat{\lambda+n&0&0&0&\cdots&0&0&0\\ n&\lambda-n&2-n&-n&\cdots&-n&-n&-n\\ 0&n-1&\lambda&3&\cdots&0&0&0\\ 0&0&n-2&\lambda&\cdots&0&0&0\\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\ 0&0&0&0&\cdots&\lambda&n-1&0\\ 0&0&0&0&\cdots&2&\lambda&n\\ 0&0&0&0&\cdots&0&1&\lambda}\\ \xlongequal{r_1}{}&\dat{\lambda-n&2-n&-n&\cdots&-n&-n&-n\\ n-1&\lambda&3&\cdots&0&0&0\\ 0&n-2&\lambda&\cdots&0&0&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\ 0&0&0&\cdots&\lambda&n-1&0\\ 0&0&0&\cdots&2&\lambda&n\\ 0&0&0&\cdots&0&1&\lambda}\cdot(\lambda+n)\\ \xlongequal{r_1\xleftarrow{+}r_2+\cdots+r_n}{}&\dat{\lambda-1&\lambda&\lambda&\cdots&\lambda&\lambda&\lambda\\ n-1&\lambda&3&\cdots&0&0&0\\ 0&n-2&\lambda&\cdots&0&0&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\ 0&0&0&\cdots&\lambda&n-1&0\\ 0&0&0&\cdots&2&\lambda&n\\ 0&0&0&\cdots&0&1&\lambda}\cdot(\lambda+n)\\ \xlongequal{r_2\xleftarrow{+}r_3+\cdots+r_n}{}&\cdots\cdots\\ \xlongequal{r_{n-1}\xleftarrow{+}r_n}{}&\dat{\lambda-1&\lambda&\lambda&\cdots&\lambda&\lambda&\lambda\\ n-1&\lambda+n-2&\lambda+n&\cdots&\lambda+n&\lambda+n&\lambda+n\\ 0&n-2&\lambda+n-3&\cdots&\lambda+n&\lambda+n&\lambda+n\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\ 0&0&0&\cdots&\lambda+2&\lambda+n&\lambda+n\\ 0&0&0&\cdots&2&\lambda+1&\lambda+n\\ 0&0&0&\cdots&0&1&\lambda}\cdot(\lambda+n)\\ \xlongequal{c_n\xleftarrow{-}c_{n-1}}{}&\dat{\lambda-1&\lambda&\lambda&\cdots&\lambda&\lambda&0\\ n-1&\lambda+n-2&\lambda+n&\cdots&\lambda+n&\lambda+n&0\\ 0&n-2&\lambda+n-3&\cdots&\lambda+n&\lambda+n&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\ 0&0&0&\cdots&\lambda+2&\lambda+n&0\\ 0&0&0&\cdots&2&\lambda+1&n-1\\ 0&0&0&\cdots&0&1&\lambda-1}\cdot(\lambda+n)\\ \xlongequal{c_{n-1}\xleftarrow{-}c_{n-2}}{}&\cdots\cdots\\ \xlongequal{c_2\xleftarrow{-}c_1}{}&\dat{\lambda-1&1&0&\cdots&0&0&0\\ n-1&\lambda-1&2&\cdots&0&0&0\\ 0&n-2&\lambda-1&\cdots&0&0&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\ 0&0&0&\cdots&\lambda-1&n-2&0\\ 0&0&0&\cdots&2&\lambda-1&n-1\\ 0&0&0&\cdots&0&1&\lambda-1}\cdot(\lambda+n)\\ ={}&(\lambda+n)D_{n-1}(\lambda-1)\\ ={}&(\lambda+n)(\lambda+n-2)D_{n-2}(\lambda-2)\\ ={}&\cdots\cdots\\ ={}&\prod_{i=0}^n(\lambda+n-2i) \end{align*} $$ 思路 2：https://math.stackexchange.com/a/340611
思路 3：记 $$ A=\mat{0&1&0&\cdots&0&0\\ n&0&2&\cdots&0&0\\ 0&n-1&0&\cdots&0&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&\cdots&0&n\\ 0&0&0&\cdots&1&0} $$ （该矩阵被称为 Kac matrix）
考虑 $Ax=\lambda x$，其中 $x=\mat{x_0&\cdots&x_n}^\top$。具体写成： $$ \left\{\begin{align*} x_1&=\lambda x_0\\ nx_0+2x_2&=\lambda x_1\\ (n-1)x_1+3x_3&=\lambda x_2\\ \cdots&\cdots\\ x_{n-1}&=\lambda x_n \end{align*}\right. $$ 令 $f(t)=\sum x_it^i$，可以写成 $t(nf-tf^\prime)+f^\prime=\lambda f$ 即 $$ \frac{f^\prime(t)}{f(t)}=\frac{nt-\lambda}{t^2-1}=\frac{n+\lambda}{2(t+1)}+\frac{n-\lambda}{2(t-1)} $$ 两端同时积分得 $$ f(t)=C(t+1)^{(n+\lambda)/2}(t-1)^{(n-\lambda)/2} $$ 也就是说，仅有这些 $f$ 展开可以作为 $x$，且这样的 $f$ 还需满足没有超过 $x^n$ 的项，因此只能有 $|\lambda|\le n$ 且 $\lambda$ 为与 $n$ 奇偶的整数。
证明：如果一个方阵 $A$ 只有行列异奇偶的位置非零，则其特征值一定正负成对出现。
考虑 $D=\operatorname{diag}(1,-1,1,-1,\cdots)$。注意到 $D^{-1}AD=-A$。因此，若 $Av=\lambda v$，则 $$ A(Dv)=(AD)v=-(DA)v=-D(Av)=-D\lambda v=-\lambda(Dv) $$
求 $$ A=\mat{b&c&0&\cdots&0&0\\ a&b&c&\cdots&0&0\\ 0&a&b&\cdots&0&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&\cdots&b&c\\ 0&0&0&\cdots&a&b} $$ 的特征值与特征向量。
我们知道， $$ \dat{A}=\left\{\begin{aligned}&\frac1{\sqrt\Delta}\left[\left(\frac{b+\sqrt\Delta}2\right)^{n+1}-\left(\frac{b-\sqrt\Delta}2\right)^{n+1}\right],&\Delta\ne0\\ &(n+1)\left(\frac b2\right)^n,&\Delta=0\end{aligned}\right. $$ 如果 $ac=0$，那么唯一的特征值为 $b$，否则 $$ \lambda=b-2\sqrt{ac}\cos\frac{k\pi}{n+1}\;(k=1,\cdots,n) $$ 特征向量似乎有点难。
求循环矩阵 $\Set{a_{(n-i+j)\bmod n}}$ 的特征值与特征向量。
这个反倒很简单，既然知道求行列式的套路是 $$ \mat{a_0&a_1&\cdots&a_{n-1}\\ a_{n-1}&a_0&\cdots&a_1\\ \vdots&\vdots&\ddots&\vdots\\ a_1&a_2&\cdots&a_0}\mat{\omega^{0\cdot0}&\omega^{1\cdot0}&\cdots&\omega^{(n-1)\cdot0}\\ \omega^{0\cdot1}&\omega^{1\cdot1}&\cdots&\omega^{(n-1)\cdot1}\\ \vdots&\vdots&\ddots&\vdots\\ \omega^{0\cdot(n-1)}&\omega^{1\cdot(n-1)}&\cdots&\omega^{(n-1)\cdot(n-1)}}=\mat{\omega^{0\cdot0}f(\omega^0)&\omega^{1\cdot0}f(\omega^1)&\cdots&\omega^{(n-1)\cdot0}f(\omega^{n-1})\\ \omega^{0\cdot1}f(\omega^0)&\omega^{1\cdot1}f(\omega^1)&\cdots&\omega^{(n-1)\cdot1}f(\omega^{n-1})\\ \vdots&\vdots&\ddots&\vdots\\ \omega^{0\cdot(n-1)}f(\omega^0)&\omega^{1\cdot(n-1)}f(\omega^1)&\cdots&\omega^{(n-1)\cdot(n-1)}f(\omega^{n-1})} $$ 那就知道特征值和特征向量分别是 $$ f(\omega^k),\,\mat{\omega^{k\cdot0}\\ \omega^{k\cdot1}\\ \vdots\\ \omega^{k\cdot(n-1)}}\;(k=0,\cdots,n-1) $$ 其中 $f(x)=\sum a_ix^i$，$\omega=\e^{2\pi\mathrm{i}/n}$。
对于 $A_{m\times n}$，$B_{n\times m}$，证明 $I_m-AB$ 可逆 $\Leftrightarrow$ $I_n-BA$ 可逆。
证 1：若 $(I-AB)C=I$，则 $(I-BA)(BC)=BC-B(C-I)=B$，故 $(I-BA)(BCA)=BA=I-(I-BA)$，故 $(I-BA)(BCA+I)=I$。
证 2：若对于某个 $x\ne 0$，$(I-AB)x=0$，则 $(I-BA)Bx=Bx-BABx=Bx-Bx=0$，其中 $Bx\ne 0$ 因为否则 $(I-AB)x=x\ne 0$。
证 3： $$ \mat{I-AB&O\\ B&I}\sim\mat{I&A\\ B&I}\sim\mat{I&A\\ O&I-BA} $$
$A^2=I$，证明 $A$ 可对角化。
$$ \begin{align*} &(A+I)(A-I)=0\\ \Longrightarrow{}&\im\L_{A-I}\subseteq\ker\L_{A+I}\\ \Longrightarrow{}&n-\dim\ker\L_{A-I}=\dim\im\L_{A-I}\le\dim\ker\L_{A+I}\\ \Longrightarrow{}&\dim\ker\L_{A-I}+\dim\ker\L_{A+I}\ge n \end{align*} $$
又知道特征空间的维数和不能超过 $n$，故 $\dim\ker\L_{A-I}+\dim\ker\L_{A+I}=n$。
这类问题可以扩展到最小多项式相关的定理：如果一个矩阵/线性变换的最小多项式为 $\prod(t-\lambda_i)^{m_i}$，那它的 Jordan 标准型中 $\lambda_i$ 对应的 Jordan 块的最大大小就是 $m_i$。
对于 Jordan 块 $J_{n\times n}$，求 $J^k$。
众所周知矩阵的幂次有一个组合意义：$A_{i,j}$ 表示 $i$ 到 $j$ 的边权，$(A^k)_{i,j}$ 表示 $i$ 到 $j$ 恰好走 $k$ 步，所有可能路径的边权之积的和。所以 $(J^k)_{i,j}$ 就是走 $j-i$，每次走 $0$ 或 $1$ 步，这个显然是 $$ \binom{k}{j-i}\lambda^{k-j+i} $$
证明对于可对角化的 $\T$ 和 $\U$，$\T$ 和 $\U$ 可同时对角化当且仅当 $\T\U=\U\T$。如果 $\T$ 和 $\U$ 可正交对角化，类似的结论也成立。
对于 $\T$ 的特征向量 $v\in\E_\lambda$，$\T\U(v)=\U\T(v)=\lambda\U(v)$ 从而 $\E_\lambda$ 是 $\U$ 的不变子空间。取 $\U$ 在其上的对角化即可。需要证明可对角化 $\Rightarrow$ 在不变子空间内可对角化，略。
正交对角化的情况，考虑 $\mathbb{C}$。还是随便取一个 $\E_\lambda$，只需证明 $\E_\lambda^\perp$ 也是 $\T$ 和 $\U$ 的不变子空间即可。首先由内积的操作知道 $\E_\lambda^\perp$ 是 $\T^*$ 的不变子空间，其次 $\T^*$ 的特征向量都是 $\T$ 的特征向量，从而 $\E_\lambda^\perp$ 也是 $\T$ 的不变子空间。