$\gdef\unit#1{\,\mathrm{#1}}$
前言
如果您真的对天文学感兴趣的话,可以考虑报这门课,但同时要做好花费一定精力的准备。这门课所需要的学习时间可能比其他 $2/3$ 学分的课多。
这门课是 $3$ 学分,$10\%$ 雨课堂随堂测验,$10\%$ 作业(需交五次),$10\%$ 观星报告(一学期有五六次观星活动),$10\%$ 微科幻写作(可以完全用 AI),$60\%$ 期末。
上课主要是按照 ppt 讲,ppt 基于的教材是 21st Century Astronomy (fifth edition),现在最新的是第七版。ppt 一千多张,知识量很大,一晚上三节课下来脑袋嗡嗡的,尤其是后半学期赶进度讲得很快,而且经常拖课。个人感觉老师很会讲,很有水平、有幽默感,但是思路比较跳跃,作为初学者很容易感觉各个知识点之间没有逻辑联系,或者单个知识点颠来倒去讲有点乱。我的笔记可能稍微梳理得清楚些,但也没法避免因为一些细碎的知识点而显得不够成系统。还是需要时间自己课后消化理解。
几个其他的任务都简单。关于观星活动有两个值得注意的点:一个是建议西操观星带个三脚架,一个是直接用自带相机拍木星和土星必然过曝,整个行星变成一个光斑。
期末个人感觉难度适中,不会考得很偏,不复习肯定会出事。$50$ 道选择,$20$ 道填空,$10$ 道简单的计算,考点全部来自 ppt,建议背 ppt,ppt 里打 * 的不考。上课时务必留意老师说“这个考试要考的啊”之类的话并记下来,甚至观星活动时都会说(例如冬季大三角),这些是真的可能会考的。
推荐 zzh 的带你速通 天文学导论和星空摄影入门、Alex_Wei 的笔记。
以下的图片与数据来源于教材和 Wikipedia。
第一节课
太阳系→银河系→本星系群→室女座超星系团→拉尼亚凯亚超星系团
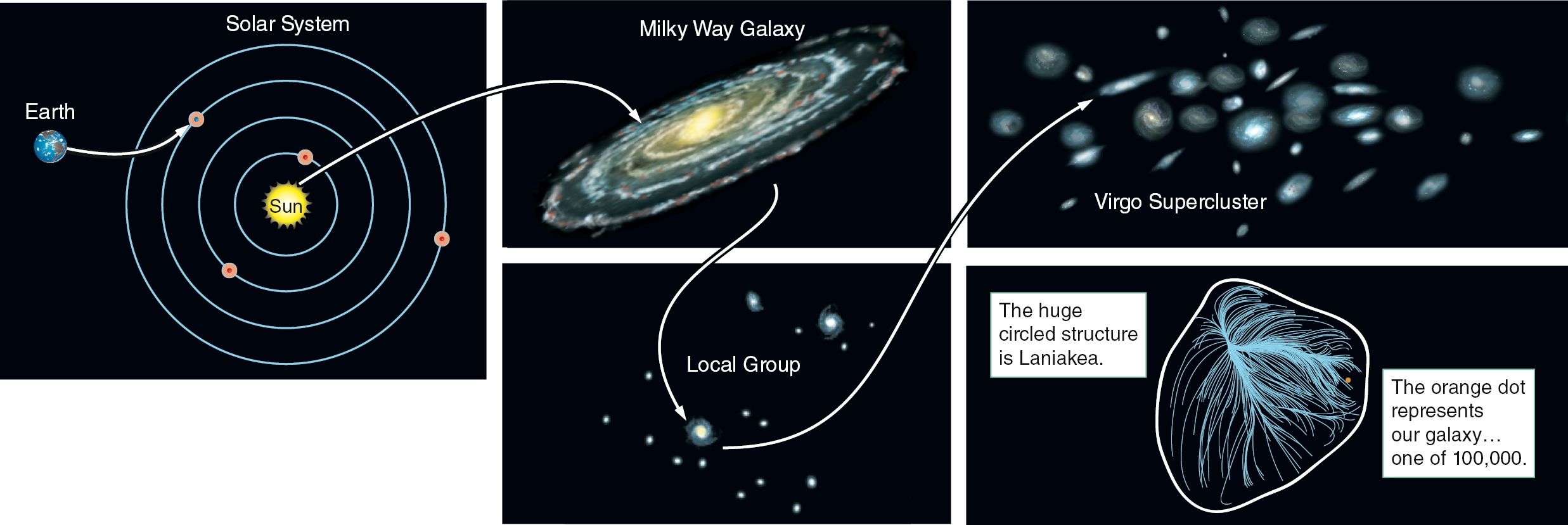
恒星、星系只占很小一部分,之间——宇宙尘埃、暗物质、暗能量。
膨胀、加速膨胀。
行星系在我们的宇宙中普遍存在。
$1\unit{AU}=1.5\times 10^8\unit{km}$,$8.3$ 光分。太阳—海王星:$60\unit{AU}$。
离太阳最近的恒星比邻星,$4.2\unit{ly}$。比邻星是红矮星,把周围的行星潮汐锁定。
太阳系离银河系中心:$2.8\times 10^4\unit{AU}$
银河系直径:$(1\sim 2)\times 10^5\unit{AU}$
银河系离仙女星系(M31,最近大星系,本星系群中最大星系):$2.5\times 10^6\unit{AU}$
麦哲伦大小星云是银河系的伴星系。
天文观测
如何定义一天(太阳日)?太阳连续两次经过从同一地点来看天空最高点(子午线)之间的时间,不等于地球自转周期。每天的时长是不一样的,这是因为地球的公转轨道不是正圆。取平均值得到平太阳日。
恒星日就是自转周期。
如何定义一年?古埃及:每年尼罗河洪水泛滥到孟菲斯城的时候,发现天狼星和太阳同时从地平线升起。这个间隔就是 $365$ 天。
基本概念
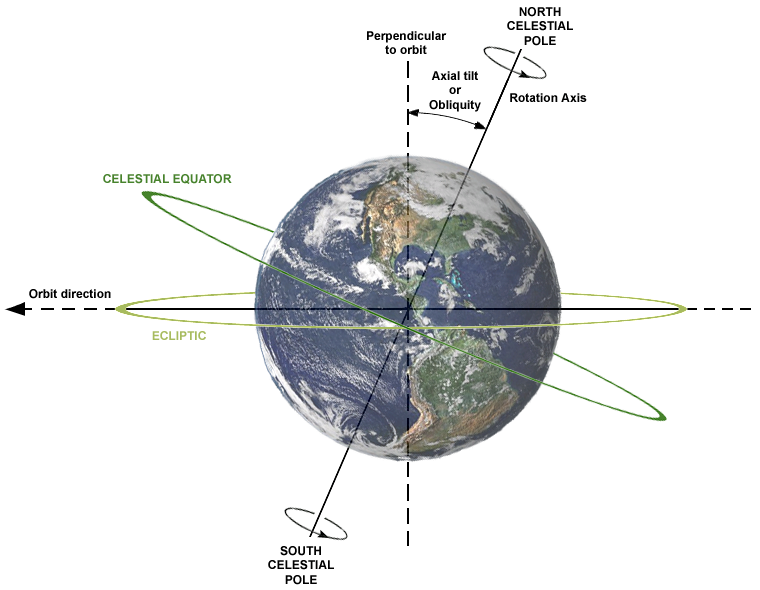
黄道是地球绕太阳公转的轨道平面。
东西的定义是,自转自西向东。东西是在地球表面特定点才说的。如果脱离特定点看整个地球,东西就是一个“旋转方向”,而不是一个矢量。
南北极的定义是,根据右手定则,得到自转的旋转向量从球心指向正北。南北相应定义,但可以脱离地球上的特定点说。
纬度是指当地地面法线对赤道面的夹角。经度指当地所在球面大圆与 0 度经度(格林尼治天文台)对应球面大圆的夹角。
地轴,就是地球的自转轴。
赤道是地球表面的点随地球自转产生的轨迹中周长最长的圆周线。赤道平面与南北极连线垂直。
转轴倾角是赤道平面与黄道平面的夹角,地球的转轴倾角约为 $23.44^\circ$。也可以定义为自转的旋转向量和公转的旋转向量的夹角,其取值可以是 $[0,\pi]$。
地球公转的方向与自转方向相同,这个“相同”的本质就是 $23.44^\circ<90^\circ$。
不要再说自转是顺/逆时针了!那会取决于观察的方向。
地磁南/北极,是地球磁场的北/南极。地磁北极,也就是地球磁场的南极,在地理北极附近,并且在持续移动。
星座
古代的星座是往图案上靠,连起来的。现在是通过将全天划分为 $88$ 个天区,每个天区对应一个星座。
星图上的信息:分区(直线为边界)、各个星座、亮度、黄道、天赤道、观测的日期时间。
(较亮)恒星的命名方式:星座 + 希腊字母(一般而言越靠前越亮)。
一般而言,一个星座的各星无物理联系,但,如果一个星位置放大了,里面有多个星,那就可能有关系了(双星系统等,例如天狼星可以算双星,它有一个伴星,是颗白矮星。很亮的星大都是多星系统),如果数量多的,就叫做星团。星团周围有光晕,是星际尘埃散射的结果。
中国古代:星官,三垣、二十八宿。
最亮的星:天狼星(大犬座 α)。
夏季大三角:织女一(天琴座 α)、河鼓二(天鹰座 α,牛郎星)、天津四(天鹅座 α)。
冬季大三角:天狼星、南河三(小犬座 α)、参宿四(猎户座 α)。
离太阳系最近的恒星系统:半人马座 α,三星。
典型造父变星:北极星(小熊座 α,三星)、造父一(仙王座 δ)。
天体的周日视运动
天球是从地球上看星空,将星空假想成一个球面,没有半径。
星星在天球上视作固定不动(随着天球动)。太阳系内的会乱动,太阳在天球上一年绕一圈。
天球赤道,就是地球赤道平面与天球的交圆。
天球的天极,就是地轴与天球相交的两点。
在地球上任何位置,都恰好能看见天球的一半。可以认为天球作为一个“屏幕”,是自东向西转动的,那么现在可以认为地球不自转。
星轨是天体随天球转动的轨迹。
所有的星星的星轨对应平面都垂直于地轴。可以结合在地球的位置,算出哪些星在当地可以永远看到(拱极星,星轨和地平面相切),哪些星永远看不到。

上图中,小球表示地球,大球表示天球,天球从右往左转。顶部蓝点为北天极和地理北极。侧面蓝点为观察点。蓝色球面为天球可见部分。橙色实线这圈及以上为拱极星,橙色虚线这圈及以下为永远看不到的星。如果观测地纬度为 $\phi$,那么拱极星的纬度在 $\pi/2-\phi$ 以上。同时,赤道面(以及星轨面)和地平面的夹角也是 $\pi/2-\phi$。
在该点处看北边天空,星是逆时针转;看南边天空,是顺时针;看东边天空,左下—右上升起;看西边天空,左上—右下降落。
天顶,就是当地的地平面法线与天球的交点。当地的正北—正南在地球球面上的弦,就是子午线。当地—北天极(附近有北极星)与当地—地面正北的夹角,可用于推导所处的纬度。
天球动,星星动,天顶不动,子午线不动。
要描述一颗星的位置怎么办?用地平坐标系。但是星星的坐标会变……
地平坐标系是以观测地为中心点的坐标系。描述天球上的一点,可以用高度角和方位角两个参数来表示。高度角是连线与地平面的夹角,方位角是水平方向的,从正北 $0$ 度开始向东(顺时针)增加。
子午线可以对应到天球上(方位角 $=0^\circ/180^\circ$,高度角 $\in[0^\circ,90^\circ]$)。任何通过子午线的天体都处于其距观测者地平面的最高位置,称为过中天。
不同经度——看到星的时间不同,不同纬度——看到星的范围不同。只有在赤道上,才能一天看尽整个天球。
我们的时间都是太阳时,只不过经度不同。正午:太阳经过子午线的时刻,不等于 12 点,因为国家有经度上的跨度。北京时间是【东经 120 度正午对应 12 时】的时间,北京本身也不是 120 度。
正午的太阳高度角为 $90^∘−(观测地纬度−太阳直射点纬度)$。
恒星日是地球上某(任意)点,某(任意)个星连续两次过中天的时间间隔。
太阳日是地球上某(任意)点,太阳连续两次过中天的时间间隔。
天体的周年视运动
回顾一天长度不等于地球自转周期的原因(“硬币悖论”):
每天白天的同一时刻,太阳的位置是往东移动的。并且太阳日的长度是不同的。与太阳的距离越小,角速度越大,太阳日的时间越长。太阳日的时间可能小于,也可能大于 $24\unit{h}$。平太阳日就是 $24\unit{h}$。一恒星日约比平太阳日短 $4\unit{min}$。
每天夜里的同一时刻,星的位置是往西移动的,或者说,每天都会提前升起,提前通过子午线,提前落下。这个提前的时间就是 $4\unit{min}$。
在黄道附近的星座,称为黄道星座。黄道星座被分为十二个,就是现在常说的星座。但现在十二个星座和十二宫已经不对应了,是岁差导致的。
恒星年的定义:太阳相对背景星,从一处回到原处的间隔。也就是公转周期,但不是公历年,这是因为两次太阳相对天球在同一位置的时候,地球的自转相位可能是不同的。恒星年约为 $365.25636\unit{d}$(太阳日)。
回归年(太阳年)的定义:太阳两次通过春分点的间隔。由于自转轴进动的原因,约为 $365.2422\unit d$,略短于恒星年 $20.5\unit{min}$。这个差称为岁差。
总结: $$ \left\{ \begin{align*} 恒星日&=\frac{2\pi}{\omega_自}\\ 太阳日&=\frac{2\pi}{\omega_自-\omega_公}\\ 恒星年&=\frac{2\pi}{\omega_公}\\ 太阳日&=24\unit h=1440\unit{min}=86400\unit s\\ 恒星年&\approx 365.25636\times 太阳日 \end{align*} \right. $$ 可以认为,除了最后一条,其他都是定义。
我们一般的直觉,恒星日和太阳日之差,经过一年后地球刚好多转一个 $360^\circ$,它的原理是: $$ (太阳日-恒星日)\times\frac{恒星年}{太阳日}=\frac{2\pi\omega_公}{(\omega_自-\omega_公)\omega_自}\cdot\frac{\omega_自-\omega_公}{\omega_公}=\frac{2\pi}{\omega_自}=恒星日 $$
赤道坐标系
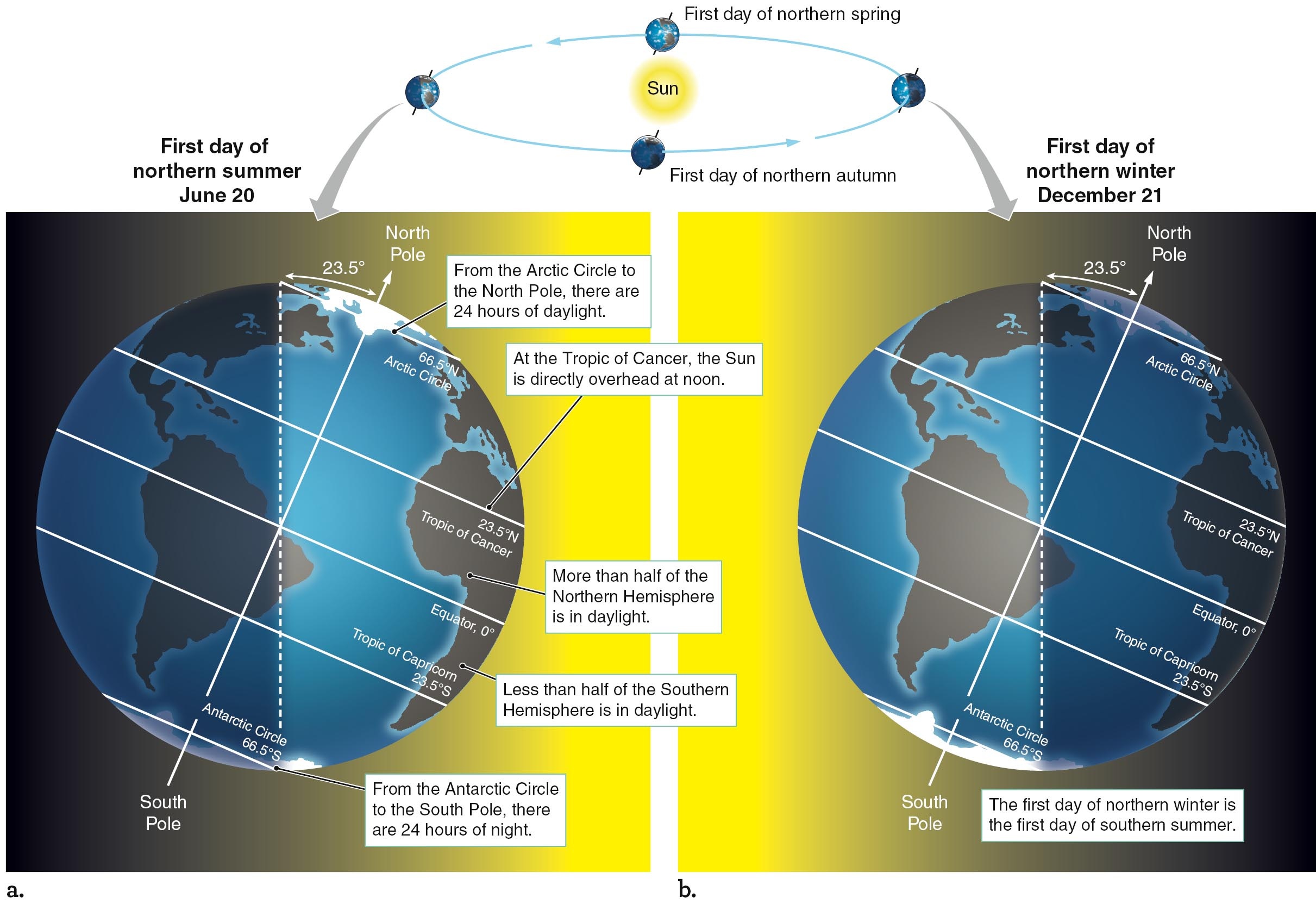
春秋分点:天球赤道与黄道的交点。春秋分是一个时刻,不是一天。


赤经(RA, α)和赤纬(Dec, δ),就是地球的经纬线在天球上的投影。特殊地,赤经的 $0$ 不是格林尼治天文台,而是春分点。赤经的单位是时间,从春分点向东转一圈为 $24\unit{h^\prime}$(一恒星日)。赤纬还是一样 $-90^\circ\sim+90^\circ$。
赤纬相同时,赤经越小,越早升起。
地方恒星时的定义:某地子午线对应的赤经。地方恒星时是不断在变的,变的速度略快于太阳时,每天增加约 $4\unit{min^\prime}$ 左右。
实际上在某一天内,各个地方在同一个当地太阳时时的地方恒星时基本是一样的,其计算思路是:由于春分时,该地 $12$ 点时的地方恒星时接近为 $0\unit{h^\prime}$,因此该地 $x$ 日 $y$ 时的地方恒星时就是 $$ [(x-春分)\times 4\unit{min^\prime}+y-12\unit{h^\prime}]\bmod 24\unit{h^\prime} $$
但是当地的时间并非绝对标准的太阳时,而是国家标准时间,因此还要算一下。例如北京的经度如果算作 $116^\circ$ 的话,恒星时就要再减去 $4^\circ\times 24\unit{h^\prime}/360^\circ$。
我们再详细说一下这个 $4\unit{min^\prime}$。每个恒星日,恒星时比太阳时多走 $$ \left(\frac{太阳日}{恒星日}-1\right)\times24\unit{h^\prime}=\frac{\omega_公}{\omega_自-\omega_公}\times24\unit{h^\prime}\approx\frac{24\unit{h^\prime}}{365.25636}\approx 3.94\unit{min^\prime} $$ 恒星时角 $\tau=$ 恒星时 $\theta-{}$恒星赤经 $\alpha$。$\tau>0$ 时,恒星在子午线以西。
岁差:太阳对地球引力的力矩,导致地球自转的同时进动。地轴会绕黄道平面法线(过地心)转。那么相应地,赤道平面也会转,春秋分点也会变(向西移动,提前到来,以 $\sim 25800\unit y$ 为周期),因此一年的时间略短于 $365.25\unit{d}$,需要通过百年不闰解决。同时,赤道坐标系也会变,即星的坐标往东移(赤经增加)。因此每隔几十年要修正。
拓展:
- 科氏力
- 太阳的 8 字形轨迹
物理基础
历史
古希腊:亚里士多德提出地心说,托勒密完善(均轮、本轮)。
中世纪:哥白尼提出日心说(反驳了一部分地心说,当时仍然支持天球事实存在,且由于精度不足,日心说的预测并不比地心说准确),第谷观测仪器+数据(介于地心日心之间),开普勒观测数据 + 三定律(完备日心说),伽利略开启近代天文学、物理学,用望远镜观察天体(彻底否定地心说,金星的盈亏,越亮越小),牛顿发现万有引力定律,第一台反射式光学望远镜。
万有引力
高中物理。略。
潮汐力
月球的公转轨道于黄道夹角为 $5^\circ$ 左右,与黄赤夹角方向相反。
地球在运动的时候,整个视作刚体,每个点的加速度相同。而地球由于相对于月球不能完全视作质点,各点受到月球的引力不同,故这里以地球为参考系,地球上的水的相同的惯性力与受到月球的不同的引力,导致了潮汐(https://www.zhihu.com/question/31294983/answer/72019418)。 $$ a_{潮汐}=\frac{2GMr}{R^3} $$ 如果月球不公转,那么基本上就是每天两个潮汐周期。但是公转就会导致略微变长($\sim 25\unit h$)。
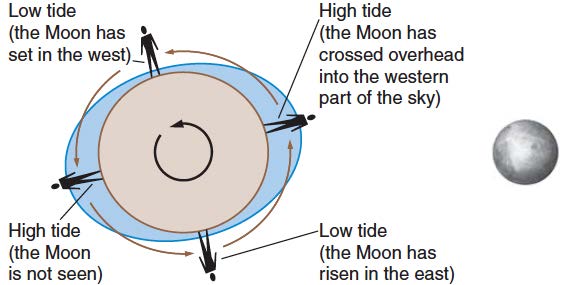
月球对地球的潮汐力导致了潮汐隆起,但是地球自转比月球公转快,这就导致隆起和地月连线不共线,这就对地球产生了与自转方向相反的力矩导致自转速度变慢,以及对月球产生了切向力导致月球公转变快从而做离心运动(https://www.zhihu.com/question/299894978/answer/3632821076)。太阳对地球也有潮汐力(是月球的),与月球共同导致大潮和小潮。地球对月球的潮汐力导致了潮汐锁定。
双星系统要考。可以证明(https://farside.ph.utexas.edu/teaching/336k/Newton/node50.html),双星系统的两个星一定是绕着它们的公共质心做(成比例的)等价于单星的运动。
两体近似:仅考虑太阳引力作用下的行星轨道的计算。其它质量对两体近似的偏离称为引力摄动。通过考虑太阳、木星土星之后仍然不对,根据引力摄动,可以预言别的行星的存在。
相对论
牛顿万有引力定律的问题:水星的椭圆轨道也会进动。但是如果只靠万有引力,只能解释一部分(火神星),需要相对论才能完整解释。万有引力只能解释弱引力的情况,而水星离太阳太近了。
相对论细节就不写了,一个提纲:
-
狭义相对论的内容,时空观。
- 速度接近光速时,长度变短,时间变慢,质量变大。
- μ 子的例子
- 计算:洛伦兹变换、质能方程。
-
广义相对论的内容(主要多处理了非惯性等效引力相关)。
-
光线在大质量天体周围的弯曲(太阳在日食时看、引力透镜),反而会变亮!
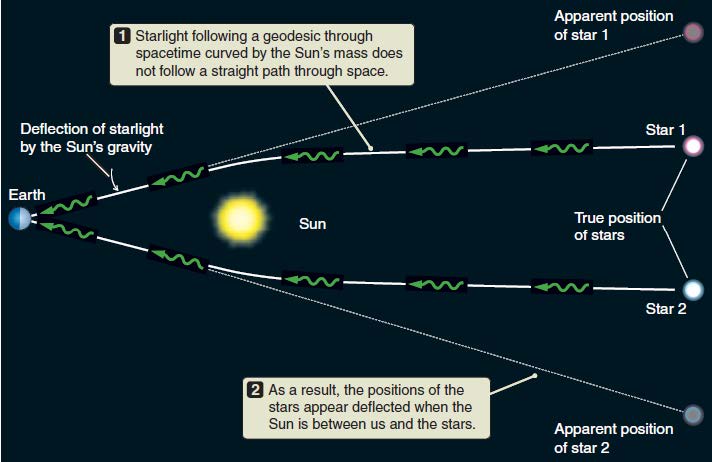
-
靠近大质量天体时,长度变短(引力红移),时间变慢(相对论时间修正)。红移公式为($\gamma$ 根据逃逸速度计算)$1+z=\gamma$。


-
辐射
电磁辐射依然是了解宇宙的主要载体,有关宇宙信息的绝大多部分来源于天体发出或反射的电磁辐射。
电磁波相关的知识:高中物理。
黑体(普朗克)辐射谱:不同温度的黑体辐射的光谱。规律:
- 温度上升,峰值波长减小,两者成反比。(从而能测星体的光谱得到其温度)
- 温度上升,(单位面积单位时间辐射出的)能量增加,能量与温度的四次方成正比。
流强 $F$:一个天体单位时间从其表面单位面积所辐射出的能量。注意这个定义和一般理解的光通量不同,它的国际单位是 $\unit{J\cdot s^{-1}\cdot m^{-2}}$。可以类比的概念应该是光出射度。
光度 $L$:一个天体单位时间的总辐射能量。类比发光强度。
亮度 $B$:观测仪器单位面积单位时间所接收到的天体的辐射能量。类比照度。
除此之外,还有距离、半径、温度等量。
通过观测,我们可以得到波长峰值和亮度。 $$ \left\{\begin{aligned} T&=\frac{2.9\times 10^6\unit{nm\cdot K}}{\textcolor{green}{\lambda_{\text{peak}}}}\\ F&=\sigma T^4\\ L&=4\pi r^2F\\ \textcolor{green}B&=\frac{L}{4\pi d^2} \end{aligned}\right. $$ 因此只靠分析光谱,只能得到 $r:d$。
辐射相关的内容在 L9 还有。
除了用 $\rm\mu m$ 等 $10^3$ 为一级的长度单位描述波长,还有一个单位 Å(埃斯特朗),是 $10^{-10}\unit m$。
当然,天体不能完全看作黑体,因为它表面的大气会吸收或发射特定频率的光子,形成光谱中的吸收线或发射线。根据这些线,可以推得其大气的化学成分及丰度。
具体关于原子能级的概念:高中物理,略。氢原子的光谱记一下。
问题:为什么吸收和发射不会抵消?回答,主要就是吸收再发射就是各个方向了,不是天体—观测者连线方向了。
原子的电离:天文学里标记的方法是用罗马数字(例如 H II = H+)。
H II 区 : 所有氢被近邻的炽热恒星的强烈紫外辐射(至少 $13.6\unit{eV}$ 才能电离)所电离的区域,是大质量恒星正在形成的标志。气体云里面是等离子体。
分子光谱:分子内的电子跃迁:可见光和紫外谱线;分子振动的变化:红外谱线;分子转动的变化:射电谱线。
多普勒效应:靠近蓝移,远离红移。 $$ \frac{\Delta\lambda}{\lambda}=\frac{v}{c} $$ 其中 $v$ 是视向速度(乘个 $\cos$)。注意只有低速情况下适用。
推导:观测到的波长定义为相邻两个波峰之间的距离。假设恒星以 $v$ 的速度远离观测者,那么相邻波峰中后一个比前一个多走 $\frac\lambda cv$ 的路程,于是 $\Delta\lambda=\frac\lambda cv$。
可以通过对比标准的谱线系列(例如氢的巴尔末谱系)来确定恒星是在远离还是靠近。
天文望远镜
伽利略发明望远镜(1609)。
折射望远镜:很简单,就是利用凸透镜成实像,和实际情况是中心对称的。没法造大,因为色散问题会愈发严重(波长越短,折射率越大,高中物理)。加长焦距可以减小色差,复合透镜可以补偿色差。
反射望远镜:利用凹面镜成实像,就没有色散问题了。但是成像位置很尴尬,所以一般再加个平面镜,在侧面(牛顿)或者底面(卡塞格林)开个小口观看。
反射望远镜的球面像差:根据高中数学,把反射镜做成抛物面的形状,才能使光汇聚到一点,结果哈勃望远镜做成了球面,就要有宇航员上去装“眼镜”,于是就有了新概念二里那篇 Trouble with the Hubble。
望远镜的主要功能不是放大,而是聚光和提高分辨率。同样长的曝光时间,同样大的像,口径越大,接受的光越多,最后光强越大。口径越大,不是看得越远,而是能看到的越暗。
口径越大,角分辨率越小。具体来说,当某处发出的光通过透镜被汇聚到光屏上一点的过程中,会发生衍射,形成艾里斑。中央亮斑的角半径为 $\sin\theta=1.22\lambda/D$,$D$ 为透镜直径,因此半径为 $f\tan\theta\approx 1.22f\lambda/D$。如果两个亮斑,一个的中心处于另一个的第一暗环以内,就认为分不清。从而定义角分辨率 $\theta=1.22\lambda/D$,单位为弧度。
课本里的话,是忽略的这个 $1.22$ 倍,$\theta=\lambda/D\unit{rad}=2.06\times10^5\lambda/D\unit{arcsec}$。
参考:https://zhuanlan.zhihu.com/p/548289357、https://www.telescope-optics.net/diffraction.htm、https://astronomy.stackexchange.com/questions/35894/how-does-diffraction-occur-in-a-reflecting-telescope
大气极限:视宁度。
胡克望远镜(1917),哈勃通过它发现宇宙膨胀,通过红移。
还有 Hale、Keck、VLT、Gemini、ESO、LBT、Subaru 等。最新:E-ELT。
为什么现在大型望远镜都是两个四个一组的?干涉仪(astronomical interferometer),分辨率可以达到相当于它们距离的大镜。
光学望远镜:望远镜(镜筒+赤道仪)+ 终端设备。终端设备(光学探测器与仪器):目镜、探测器(照相机,CCD/CMOS)、分光仪器(摄谱仪/分光仪)。
受限于大气层(反射、吸收、扰动),在地面能看到的,只有可见光、射电、部分红外与毫米波。
之所以射电望远镜口径都这么大(或者需要阵列),就是因为 $\theta\propto\lambda/D$。大的:Arecibo、FAST。
空间望远镜就可以看各波段了,但是造价太高。大的:哈勃、JWST、GMT、TMT。
THU:MUST。PKU:EAST。上交:JUST。国内最大的是 LAMOST。
太阳系
行星可以认为是恒星形成的“副产品”。
行星系是环绕一颗恒星(也可以是死亡后的恒星)的天体集合,包括行星、矮行星、小天体(卫星、小行星、彗星、流星体等)。恒星系不考虑行星,只是若干恒星,比如南门二(含比邻星)。
行星的定义:质量够大足以使自己成为球体,轨道清晰无杂物。目前有发现“流浪”行星(没有围绕恒星)。
矮行星的定义:不具有能清除轨道上其他天体的能力,别的和行星一样。
太阳系里的矮行星:谷神星是小行星带中唯一的,别的(冥王星、阋神星(直接触发了冥王星的降级)之类的)都在柯伊伯带。
彗星:来自柯伊伯带或奥尔特星云(更外围)。有彗星的轨道是扁椭圆(例如哈雷彗星),来自柯伊伯带,还有一些是双曲线(只能靠近太阳一次),来自奥尔特星云。
太阳系的形成
太阳系形成的星云假说:康德 → 拉普拉斯(天体力学之父)
太阳系的早期图景:原太阳(尚未开始燃烧氢)被一个自转着的,扁平的气体尘埃盘环绕。这个旋转的盘不仅为太阳的成长提供物质和能量(质量集中在盘中心,最后形成太阳),而这个盘中的少量剩余物质形成了太阳系的行星等其它天体。一个自转的星际云通过引力坍缩形成了太阳及太阳系。
支持星云假说的证据:
- 已观测到许多年轻恒星被气体尘埃盘(星周盘/原行星盘)环绕。这个盘本身是不可见的(发出的光不是可见光波段的),但是会散射恒星的光。另外还有喷流,垂直于盘面。我们目前看见的那些盘面的图片,都是比如毫米波段的望远镜的图像合成出来的。会发现盘是一个个圆环状,暗环就对应正在形成的行星。可以看 L1527 IRS。
- 所有行星轨道基本位于同一平面内 → 早期太阳系必定是扁平的。所有行星公转和自转方向,与太阳自转方向相同(有反例:金星、天王星,解释:随机大碰撞) → 形成行星的物质必定沿相同方向围绕太阳转动。
- 陨石是落到地球表面的年轻太阳系的遗留碎片。其结构清晰地表明,陨石(再大就发展成(小)行星)是由许多小块物质聚合而成的,被称为时间胶囊。
原行星盘是怎么形成的?关键是角动量。虽然太阳系的质量几乎全在太阳上,但角动量主要在行星(木星)上。
恒星系一开始是个星际云。一个星际云绕银河系中心公转,由于不断被恒星爆炸推挤,或与其它星际云碰撞,使得星际云有一定的轻微自转。星际云非常延展巨大,具有巨大的角动量。星际云在自引力(需要有足够的质量和密度)的作用下开始坍缩变小。由于角动量守恒,其自转随着坍缩变小而越来越快。而引力坍缩具有方向性——考虑一块物质,在垂直于自转轴的方向,它确实受到引力,但一部分用于充当向心力了,因此坍缩得慢;而平行于自转轴的方向没有向心力,因此就坍缩得快,于是就形成一个盘状。由于坍缩更快, 与外区分离的内区形成原恒星与吸积盘。外区物质首先下落到具有转动的吸积盘,然后沿近似椭圆轨道靠近原恒星。吸积盘相当于一个“中转站”,它的半径是恒星的约几千倍,同时有很大的角动量,但其大部分物质成为恒星的材料的同时,角动量大的部分,通过射流被抛回星际空间,或是等剩下到足够稀了之后,和外区一起(也是角动量很大,不然就掉进来了),就成为行星的材料。
一个可能要考的公式:角动量为 $$ L=\frac{4\pi mR^2}{5T} $$ 星体的成长:
- 微粒之间的吸附,气体将小颗粒吹入大颗粒,合并。
- 大了($100\unit m$)之后,猛烈的碰撞会导致再碎成小的;如果不猛烈,可以继续增大。
- 再大($1\unit{km}$)称为星子,它的引力可以吸引周围的小物体,不断加快增长。最后变成原行星。这一过程中有大量的撞击,这在岩质行星上留下了陨石坑。
原行星盘内热外冷(原恒星的热辐射、下落气体的引力势能、粘滞(摩擦))。这导致各种物质在不同行星上的状态不同,所以太阳星外围的行星都是气态行星(太阳系的行星排列:内区,星子由岩石和金属组成;外区,主要由岩石、金属、水冰和冰态的挥发性有机物组成)。系外行星系的行星排列并非都是如此,可能发生了行星迁移(气体导致行星角动量损失,内移,热木星;天海王星是因为木星和土星的引力散射)。

巨行星的成长:固态行星(核)一旦形成,它将继续吸积原行星盘中的气体而成长。 质量巨大的固态行星对聚集和维系氢和氦等轻元素气体具有明显的优势。强大的引力使得大质量的年轻固态行星在其周围形成“微型吸积盘”,物质(气体)通过吸积盘旋入固态行星。很多小行星就是这样被木星、土星捕获的。
还有个假说是盘不稳定性,说的是原行星盘会碎开,每个对应一个巨行星。
行星形成时从原行星盘中所获得的气体称为原始大气。巨行星能维持一开始捕获的气体,小质量行星不能。所以像地球、金星的大气层,都是次生大气,源自火山从行星内部喷出来的二氧化碳等气体,或彗星撞击。
小行星和彗星核是存活到今天的星子,几乎保持太阳系刚形成时的状态。火星和木星之间的小行星带,是因为受到木星强大引力的搅动没能凝聚为一个行星。
系外行星
2017 年人类首次在太阳系内发现系外天体 Oumuamua。
行星很常见,但由于小而暗弱,且靠近明亮的恒星,所以探测很困难。
发现的第一颗系外行星:1995 年,飞马座 51 b,视向速度法。目前已经确认的系外行星已有数千颗。
系外行星是绕恒星公转的且质量小于 $13$ 倍木星质量的天体。褐矮星是大于 $13$ 倍木星质量,小于 $0.08$ 倍太阳质量,性质类似于木星。恒星是大于 $0.08$ 倍太阳质量,这样才能氢核聚变。
发现行星的方法:
- 视向速度法:观察恒星光谱吸收线的周期性的频移。就是认为行星和恒星形成一个双星系统。
- 凌星法:当行星运行到恒星前面时,会遮挡很小一部分恒星光,从而使得恒星周期性地变暗。可以用于计算行星大小。
- 微引力透镜法:当一颗恒星及其行星从远处背景恒星前经过时,引力透镜效应增强背景恒星的亮度,从而能够显示恒星及其行星的存在。可估算行星的质量,还能发现流浪行星。注意,可以区分恒星本身亮度变化与引力透镜造成的变化:引力透镜对各波段的影响(亮度变化比例)是一样的,自身变化(比如温度变化)显然是不同的。
- 直接成像法:在天文望远镜上加装星(日)冕仪,降低恒星亮度,直接拍摄行星。
- 天体测量法:直接观测恒星位置受行星影响的周期性变化。
以下是目前已知的系外行星的分布:

关于凌星法,这里有一个问题,就是,为什么太阳看起来是圆盘上各处亮度相同的?这是因为太阳是朗伯辐射体,对于一个小面 $\mathrm{d}a$,如果观察角度(观察点与其连线,和面的法向量的夹角)为 $\theta$,则看到的发光强度就是 $I\cos\theta$。朗伯辐射体的特性是,“视亮度”(观察到的光通量与视大小之比)与观察角度无关,因为这个 $\mathrm{d}a$ 从 $\theta$ 角度来看,面积就只剩下 $\mathrm{d}a\cos\theta$ 了,除一下刚好抵消。因此我们可以严格地说,凌星法中,理论上,太阳亮度的减少量就正比于遮住的面积。实际上的话太阳的远离更复杂些,还有周边昏暗效应,所以拍出来的图片还是周围暗。
历史:
- 1992 年:发现至少三颗围绕中子星转的系外行星。
- 1995 年:发现围绕主序星(飞马座 51)旋转的系外行星。方法:视向速度法。
- 2021 年:首颗被确定的河外行星,M51-ULS-1b。
- 后续发现方法:开普勒望远镜,发现首批地球大小的系外行星(凌星法,确定大小);进一步证认:地面大口径望远镜(视向速度法,确定质量)。
科学家还是很关心类地行星。要有生命产生,需要有液态水的存在(在宜居带内),和地球大小差别不太大,围绕类似太阳的恒星转。也会考虑光谱与地球的类似。
开普勒 452b:第一个地球 2.0(后来发现观测到的信号是假的?)
比邻星:至少三颗行星,且都已被潮汐锁定,不太可能有生命。且红矮星耀斑爆发剧烈,容易杀死行星上的生命。
太阳
太阳为什么是稳定的?太阳的结构是向外压力(气体产生)与向内引力平衡的结果。在向外辐射能量的同时,核心进行的核聚变补充能量,形成平衡。压力、密度与温度向太阳中心增加。
太阳通过热核聚变把质量转化为能量。(氢)核聚变需要足够高的温度与密度,克服电斥力,使强相互作用力将两个质子结合在一起,产生新原子核与其它粒子,释放能量。链式反应(PP 链)。四个氢原子聚变成一个氦原子。能量产生的根源。核聚变比化学燃烧的能量转换效率高很多。其他核聚变方式:碳氮氧循环。
太阳的主序寿命约为 $10^{10}$ 年,目前已过了约一半。
太阳中心产生的能量去向:
- 中微子直接逃逸到宇宙空间
- 加热太阳内部
- 向外转移到太阳表面辐射出去
能量传输方式:主要是辐射与对流。
层:核反应区 → 辐射区 → 对流区 → 太阳大气
核反应区是等离子态,核聚变只在核反应区发生。
光子在辐射区的传播比较困难,需要与电子碰撞很多次才能到对流区,这部分的气体更密了,就会把光子吸收,变热,往外飘,辐射出能量,再往内沉。对流的强弱取决于温度梯度与不透明度。气体的对流运动在光球层形成被称为日面米粒组织的斑驳图像。有点像味噌汤
到大气之后,光子又能自由运动了,再过约 $8.3\unit{min}$ 到地球。一个光子从产生到太阳表面,得经过数万年的时间,并且是由伽马射线变成了可见光左右(包括红外和紫外)波段的。
可以通过观测中微子(不受太阳气体影响)来分析太阳内部核聚变的情况。中微子探测器都在地底下深处。建立的太阳物理模型,其他数据都与观测相符,但观测到的中微子数量(单位流量)只是预言的 $1/3$。解释是中微子有质量,存在中微子振荡,中微子在 $e$、$\mu$、$\tau$ 三类中转化,而观测只能观测到 $e$(电子中微子)。
太阳表面不同的小区域同时发生很多不同频率的振荡。
太阳大气从内到外分为光球层、色球层和日冕。
太阳的密度和温度从内向外降低,但在色球层温度增高,在日冕温度突然增高,密度突然减小。
我们看到的太阳是光球层。温度约 $5780\unit K\,(6600\unit K\to 4400\unit K)$,厚 $500\unit{km}$,相比别的层较薄(所以太阳边界清晰)。临边昏暗效应就是因为在边上只有浅的部分的光,量和温度都小。从光球层发出的光会被太阳大气吸收部分,可以通过分析太阳光谱得到太阳大气的成分。
光球层之上的 $1500\unit{km}$ 厚的区域称为色球层,温度 $4500\unit K\to6000\unit K$。要观测必须把光球层的影响去掉,需要特殊的望远镜。它是深红色的,不是光滑的球状而是针状等离子喷泉。
在色球层外部的约 $100\unit{km}$ 的区域(过渡区),气体温度急剧上升,在此区域之上是太阳大气的最外层日冕,密度低,温度极高(百万 $\unit K$),延伸至 ${\sim}10$ 倍太阳半径。
太阳活动:太阳黑子、日珥、太阳耀斑、拱形冕环。和磁场有关。由于太阳是等离子体,故变化的电场产生磁场,导致复杂的太阳磁场结构。另外,太阳存在较差自转(不同纬度,不同深度转动角速度都不同),以及对流,因此磁场被扭曲,产生这些“不稳定”的现象。
太阳黑子温度也没那么低(可以用 $F\propto T^4$ 算)。它的大小可以达到地球直径的数十倍。太阳光谱观测表明太阳黑子磁场很强(塞曼效应)。磁场垂直进出的地方出现黑子,这种地方和附近的等离子体无法对流,温度变低。太阳黑子经常成对出现,每对黑子皆有在太阳表面上方的拱形磁力线相连,体现为冕环。两个黑子磁场方向相反,南北半球黑子极性相反。黑子寿命 $<11$ 天。日珥也是磁场的体现。总之可以认为表面等离子体的纹理反映磁感线(

太阳耀斑:最剧烈的太阳活动形式,一次喷发的磁能与日珥相当(但是耀斑时间短,日珥时间长),喷出速度极快。
日珥和耀斑由磁重联造成。
日珥和耀斑的日冕物质抛射到地球大气形成极光。日冕物质抛射一般都需要日珥和耀斑,但日珥和耀斑不一定有日冕物质抛射。喷射的东西包括磁能、高能射线、热等离子体。
最有名:1859 年的卡林顿事件。
太阳风相对温和,持续,它是由磁场指向外部的冕洞(几乎无高能辐射)造成的。
黑子反映太阳活动强度,$11$ 年周期,两侧黑子越靠近赤道,强度越弱。黑子数最多的年称为太阳峰年。蝴蝶图。太阳磁极每一周期翻转。

太阳系中的各行星
这部分是自学不考内容,主要就是讲各行星的地质特点,可以看 zzh 的博客。
恒星
一些定量分析的方法
恒星是一个自引力束缚的气态球。氢的燃烧(核聚变)是恒星的主要阶段,称为主序阶段。
恒星的视差 $p$(小学就学过啦):在相隔半年时间内,恒星视位置变化的角大小的一半,或者应该说是恒星在天球上最两侧的角差(因为有的半年可能不对,必须是地日连线垂直于日星连线),小到角秒级。
$1\unit{arcsec}$ 对应的距离为 $1\unit{parsec}$(秒差距),就是 $1\unit{parsec}=d_{\text{地日}}\cdot\cot(1\unit{arcsec})\approx 3.26\unit{ly}$。
因为 $\cot$ 算起来麻烦,所以考虑近似。$p$ 和 $d$ 在数值上的关系: $$ d=d_{\text{地日}}\cdot\cot p=d_{\text{地日}}\cdot\cot(1\unit{arcsec})\cdot\frac{\cot p}{\cot(1\unit{arcsec})}\approx 1\unit{parsec}\cdot\frac{\mathrm{arcsec}}{p} $$ 什么?你不知道为什么能这样 $\approx$? $$ \frac{\cot k\theta}{\cot\theta}=\frac{\tan\theta}{\tan k\theta}=\frac{\theta+\Omicron(\theta^3)}{k\theta+\Omicron(\theta^3)}=\frac{1+\Omicron(\theta^2)}{k+\Omicron(\theta^2)}\sim\frac1k $$ 简而言之,可以写成 $d=1/p$。
视星等:体现视亮度。最初制定时分为 $1\sim 6$ 等,$1$ 等最亮,$6$ 等最暗,$1$ 是 $6$ 的 $100$ 倍,也就是一等 $\sqrt[5]{100}\approx 2.512$ 倍。恒星视亮度用视星等表示,即以恒星视亮度的对数来表示。同一颗星,不同波段的视星等不同。
实际上星等都是小数,还能是负的。如果 $0$ 等星的视亮度为 $b_0$,那么 $m$ 等星的视亮度为 $$ b=b_0{100}^{-m/5} $$ 也可以反推视星等 $$ m=-5\log_{100}\frac{b}{b_0}=-2.5\log_{10}\frac{b}{b_0} $$ 例如从地球上看太阳,$m\approx-26.7$。
不同观测仪器有不同的可观测最暗星等,比如眼睛是 $6$。
低光度恒星数量比高光度恒星数量多得多,比太阳光度高的恒星只占总样本的 $20\%$ 这样(而且暗恒星只会发现得越来越多)。
绝对星等:体现光度,放在标准距离处的亮度。距离模数 $=$ 视星等 $-$ 绝对星等 体现距离。
将星放在 $10\unit{parsec}$ 处的视星等,就等于绝对星等。 $$ M=-2.5\log_{10}\frac{L}{4\pi(10\unit{parsec})^2b_0} $$ 距离模数通过光度和视亮度给出距离: $$ m-M=-2.5\log_{10}\frac{b\cdot4\pi(10\unit{parsec})^2}{L}=-2.5\log_{10}\frac{\frac{L}{4\pi d^2}4\pi(10\unit{parsec})^2}{L}=5\log_{10}\frac{d}{10\unit{parsec}} $$ 所以从数值上来说($d$ 单位 $\mathrm{parsec}$) $$ m-M=5\log_{10}d-5 $$ 分析恒星的表面温度固然可以分析光谱,但更简单的方法是直接用两个窄波段滤光片,看这两个波段的亮度的比值得到温度。这两个波段的视(无所谓)星等之差,被称为色指数。定性地看,表面温度越高,色指数越小。色指数与温度没有简单的比例关系,只能用 Ballesteros’ formula 近似。
所以,要确定一颗星的半径,实操上可以用以下方法:
- 通过周年视差 $p$ 确定距离 $d$。
- 测得视亮度 $B$,求得光度 $L=4\pi d^2B$。
- 测得色指数 $B\text{-}\!V$ 确定温度 $T$。
- $R^2=L/4\pi\sigma T^4$。
双星系统的推导等下学期普物一,这里就记两个公式:一个是,轨道半径(周长)与质量成反比,一个是开普勒第三定律 $$ T^2=\frac{4\pi^2A^3}{G(m_1+m_2)} $$ 实际应用时, $$ \frac{m_1+m_2}{M_{\odot}}=\frac{A_{\rm AU}^3}{T_{\rm years}^2} $$ 根据发现的方法,双星分为四类:
- 目视双星。离地球较近或两星距离较远,可以直接观测位置来分析。
- 分光双星。虽然无法直接区分两星,通过分析光谱可以发现两组多普勒效应偏移相反的谱线,就可以确定是双星。通过得到的视向速度(多普勒速度)曲线,可以得到周期、轨道半径等。考试题应该都会假设地球在其轨道平面上。如果速度关于时间轴对称($\max=-\min$),那么就是圆轨道(但是我感觉椭圆轨道也可能这样啊……)。这种曲线图要会读,可能会考。
- 食双星。其关键是,当地球和两星共线时,视亮度会降低。降低程度取决于哪颗在前,因此有主食和次食。
- 天体测量双星。如果一颗星似乎绕着空的位置在转,就意味着可能存在另一颗没观测到的星。
光谱型:从热到冷 $\rm OBAFGKM$,每个内部又有 $0\sim 9$ 级。一开始是按照氢的谱线分类的。

赫茨普龙—罗素图
赫—罗图:横坐标是温度,纵坐标是光度,都是对数坐标。由于 $$ \log R=\frac12\log L-2\log T+C $$ 因此在图上,等半径线是斜率为正的直线($T$ 反过来了)

有 $90\%$ 的恒星(主序星)位于主序带上,它们就是处于氢燃烧阶段。它们处于主序带的哪里,取决于它们的质量。太阳是 $\rm G2V$,$\rm V$ 表示主序。
这张图一个有用的东西是,原来测一个主序星的半径,需要先测距离,但是太远的话视差就太小了。现在只需分析光谱得到温度,就可以直接推得光度和半径,还能反推距离。当然这个关系的参数需要一些已知的近邻恒星样本。这个叫第一类标准烛光法,或分光视差法。
质量也可以推:

质光关系 $L\propto M^{3.5}$,半径 $R\propto M^{0.8}$。
主序恒星只需要温度就可以确定了,非主序恒星仍需要光度,光度不好测,还是只能分析光谱。比如巨星大气压力小,故谱线宽度宽。
- 主序恒星揭示恒星的属性及运行机制。
- 非主序恒星揭示恒星如何形成、演化及消亡。
实在太远的恒星,光太微弱了,观测得利用引力透镜。
星际介质与恒星形成
恒星总是一批批形成,也就是星团。在星团里,$d$、化学成分基本都一样,所以研究时只需关心质量。
星系内的恒星仅占据很小的空间。星系内的空间叫做星际空间(星系间的就是星系际空间),充满了星际介质,$\sim90\%$ 是氢,$\sim10\%$ 是氦,极少数是重元素,这些气体称为星际气体。星际介质非常稀薄,但相对整个宇宙的平均水平又高些。星际介质中 $\sim1\%$ 质量的物质是称为星际尘埃的固体颗粒,这些颗粒也很小,最多跟紫外线波长差不多。
在致密、冷的环境中,尘埃会粘合在一起,还可吸附其它的原子和分子。
星际尘埃会导致尘埃效果/星际消光(散射 + 吸收),影响观测。在可见光波段附近,波长越长,消光效果越弱(船喻)。所以,看到的星光偏暗、偏红——星际红化。所以需要修正。
既然星际尘埃也会吸收光,所以它也有黑体辐射,反正就是温度比较低,主要在红外波段。
大约一半的星际介质集中在 $\sim2\%$ 的星际空间中,这些相对致密的区域称为星际云,其余的被称作云际气体。越热的星际气体越少。炽热的云际气体主要是被近邻的超新星爆炸加热产生。
氢:
- H II。星际云,恒星形成。
- H-α。云际气体产生的最强的可见光谱线。
- 中性氢,产生 $21$ 厘米辐射,不受尘埃影响,有利于研究银河系的结构。
H II 区是被大质量、炽热、极亮的 $\rm O$ 型和 $\rm B$ 型恒星的强烈紫外辐射所电离的相对致密的星际云。在星际云最致密的核心区,分子可以存活。这些暗云被称为分子云,是恒星形成的场所。这些地方温度反而是低的,才能使分子稳定。说密,它密度也超不过我们抽的真空中剩余的分子密度。分子发射线(射电、红外)是分子(云)的指纹。分子云仅占银河系星际空间的 $\sim0.1\%$。最大的分子云称为巨分子云。
分子云里除了 H,还有 CO 和少量有机物。
可见光波段的暗斑的轮廓体现了分子云的轮廓(全被致密的尘埃吸收了),从红外波段看就可以透过看。分子的射电辐射不受星际尘埃的影响,是研究最致密最不透明的分子云的核心的窗口。
分子云的自引力比向外的压力小很多,但因为周围有更热的云际气体,所以就使它维持着不扩散。如果分子云质量足够大、足够致密、足够冷,其自引力就会相对于压力更显著,才会发生引力坍缩。一旦开始坍缩,就会越来越快。坍缩是不均匀的,所以分子云会裂变成多个分子云核(因此会有很多星团,一堆在一起的恒星)。分子云核中心坍缩比外层坍缩快,中心与外层分离,然后后面就是和太阳类似的故事,原恒星,吸积盘……
把原恒星和其最终形成的恒星比较。原恒星比恒星大很多、亮很多,但表面温度低(辐射红外),还在为氢聚变积累温度。坍缩是缺乏能量的体现。这个时候中心其实是有聚变的(氘(产生于大爆炸,只消耗不产生)和氕聚变成氦 3,但温度还是小于氢聚变所需的温度 $\sim10^7\unit K$),中心核发生对流,暂时阻止气体下落。等氘耗尽后,继续加速下落。等到足够小,密度足够大,温度足够高时,氢聚变开始,不再坍缩,结构稳定后,进入主序阶段。
褐矮星是质量过小使温度不足以使核聚变发生的情况,情况介于木星和太阳之间。就一直发射红外波段的光。温度从高到低分为 $\rm LTY$ 型(接在光谱型那个后面)。
小质量原恒星收缩时,内部变热,但其表面温度基本维持不变(负氢离子理论),于是光度下降。我们可以在赫—罗图上画出原恒星变成恒星时物理量的变化,称为演化程。

林忠四郎线特指原恒星到主序恒星的这一族演化程。
原恒星的喷流(还有星风、外向流)驱散分子云核与吸积盘,终止物质流入原恒星。原恒星的喷流是最菜的。喷流撞击到星际介质,加热星际气体(弓形激波)产生发光的气体结,称为 HH 天体。创生之柱的红外波段照片中的柱子里的红色点点就是这个东西。
太阳形成需时大约三千万年。
在主序阶段缓慢燃烧的过程中,恒星在赫罗图上向左上移动,光度增加,表面温度降低(为什么我查到有些说温度也升高?),半径变大。
质量越大,恒星的主序寿命越短(原恒星的寿命也最短)。具体的定量关系没法给出。对于与太阳性质相似的恒星: $$ \tau_{\text{MS}}=10^{10}\unit{y}\cdot\frac{M/M_\odot}{L/L_\odot} $$ 根据质光关系, $$ \tau_{\text{MS}}\propto M^{-2.5} $$ 氦与氢的比,离中心越近越大,主序阶段燃烧越后越大。当核心的氢越来越少,核心压力就减小(氦目前可不会燃烧(聚变),它需要高得多的温度),开始坍缩,这会导致中心燃烧效率增加,压力增加,外部就膨胀了。核心的氢尚未耗尽时,这一过程是缓慢的(基本稳定),等到完全耗尽了变成红巨星的过程就快了。所以现在整个的情况就是,核心收缩,外部扩张。十亿年后,地球已不宜居。

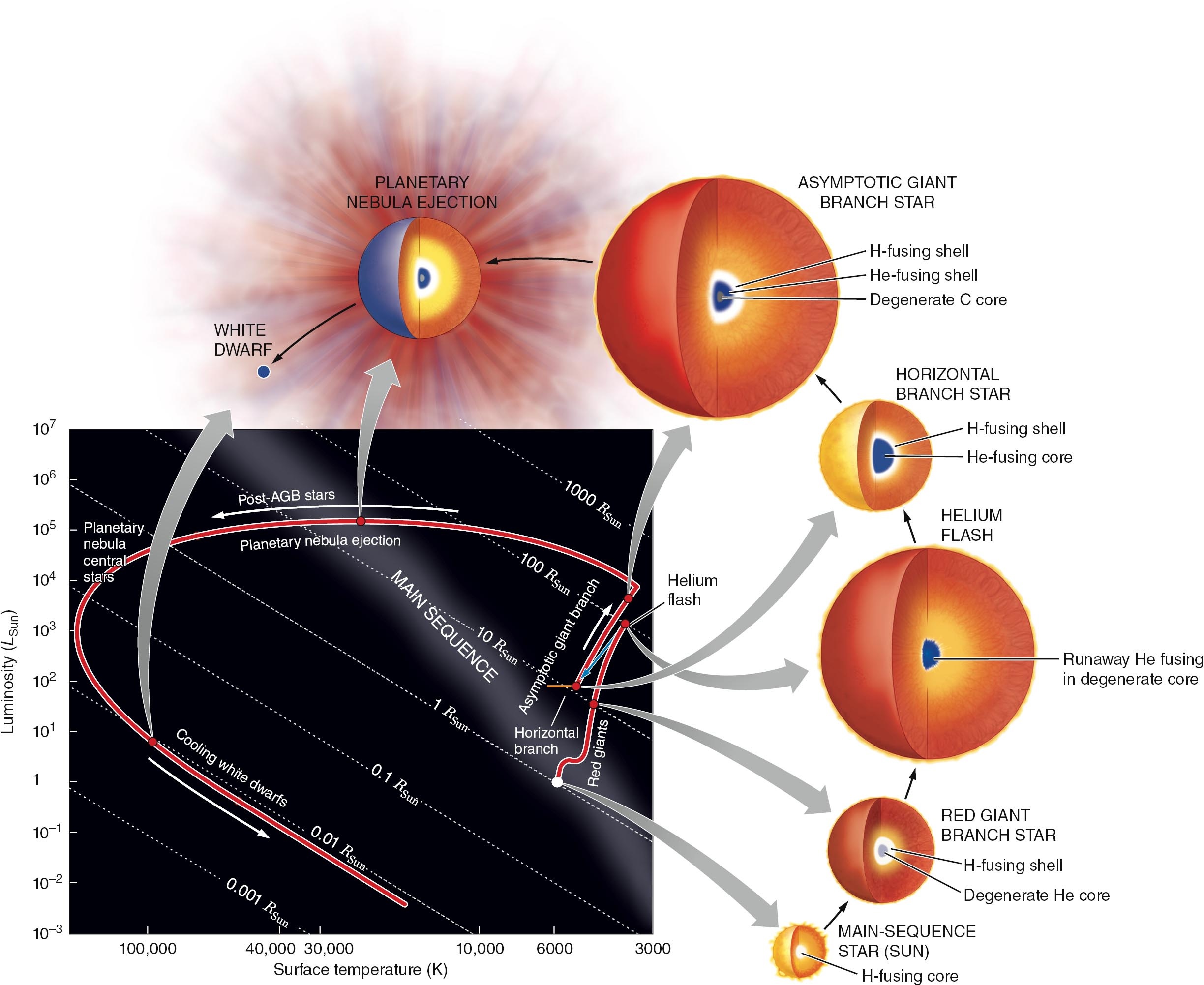
主序阶段之后——小质量恒星
当核反应区的中心一块很小的区域的氢彻底烧完后,这部分再坍缩也没法促进燃烧了。所以氦核会不断坍缩,坍缩至电子简并状态(??都说了是氦核,为啥会有电子?),会提供电子简并压力抵抗引力。所以现在分成三个区域——简并态的氦、氢壳层(也属于核反应区,还在燃烧)、氢包层。既然氦坍缩了,氢壳层就会缩小,引力增加,燃烧加快。所以还是接着,光度增加、温度降低、半径变大。氦核质量增加和氢壳层燃烧加快互相促进,是一个滚雪球的过程。
恒星脱离主序后的第一个阶段称为亚巨星,表面温度下降。当温度下降一些后,又由于负氢离子理论,温度又开始维持,但继续变大变亮,这个是红巨星阶段。
虽然表面温度变低再不变,但氦核区的温度是持续升高的。当温度到一亿 $\mathrm{K}$ 左右时,开始氦核聚变,也称为 3α 过程(He→Be→C)。简并物质是很好的热导体,一旦氦核的中心开始燃烧,整个氦核一下子就被“点燃”了。但是由于热压相比电子简并压力可以忽略不计,故氦核几乎不膨胀。于是温度升高与燃烧互相促进,所以说简并氦核的燃烧是失控的,称为氦闪。当然最后热压会大到超过电子简并压力,起主导作用,导致氦核内爆,膨胀冷却,电子简并很快被解除。氦闪从外面是看不出的。氦闪这个过程时间很短,只有几小时。氦闪后,氦核和氢壳层的引力减弱,压力减小,导致核反应率明显降低,表面明显变暗,但是实际上温度升高(我也不知道为啥),称为水平支恒星。
这个状态又会稳定一段时间,同时进行氢和氦的燃烧,但相对主序阶段短很多。离开水平支阶段,也就是碳核开始坍缩至电子简并态,进入渐近巨星支阶段,再次变大变亮但变暗,同样可能发生碳闪。太阳由于质量不够,无法达到碳核聚变的温度。
随着恒星膨胀得越来越大,导致其外层的逃逸速度越来越小,外层物质越来越容易逃逸到星际空间。于是恒星就慢慢只剩下了碳核、氦燃烧壳层、氢燃烧壳层了,光度依然很高,温度开始越来越高,这个阶段称为后渐近巨星。现在的温度足以辐射紫外波段的光,它会加热并电离被抛射出的气体,使气体电离发光,形成行星状星云(和行星半毛钱关系都没有)。最后燃烧完了,碳核就变成白矮星了,质量约为原来恒星的 $\sim70\%$。当然球表面还是有氦的,碳会和氦聚变形成氧,太阳未来会变成碳—氧白矮星,碳核收缩为大小在地球这样,压力与引力平衡,不再变小,只是还在往外辐射能量。最后没东西辐射了就变成黑矮星。
如果太阳质量损失量比较大,地球的轨道就会外移,继续围绕那时的太阳公转;否则地球会因与气体的摩擦降低速度,坠入太阳中心,这会使太阳短暂地变大变亮。
主序阶段之后——大质量恒星
大质量恒星的主序阶段氢燃烧以碳氮氧循环为主。
即便在主序阶段,高辐射压导致大质量恒星猛烈地抛射其外层物质,产生高速星风,显著影响恒星的演化。
由于质量大,温度在氦、碳进入电子简并状态前就已经达到对应的核聚变温度了,因此不发生简并,核燃烧由一种元素平稳过渡到另一种元素。元素越重,燃烧的持续时间越短。大质量恒星在脱离主序带之后被称为红超巨星。

许多红超巨星都是变星。恒星在赫罗图上形成不稳定带,周期性交替膨胀与收缩,引起其光度和颜色(表面温度)相应改变,这样的变星称为脉动变星。这种周期性变化的原因很复杂,主要是跟氦的电离与复合有关。详见 https://www.zhihu.com/question/61799031/answer/3481304995。在变动的过程中,是小热亮↔大冷暗。脉冲变星有很多类,代表性的有 I 型造父变星(黄超巨星)、II 型造父变星(小、水平支)、天琴 RR 型变星(小、水平支)。每一类都有一个周光关系(都是光度与周期正相关)。也就是说,只要观测出周期,就可以得到光度,从而这个变星可以作为标准烛光。
铁核永远不会燃烧,这是因为铁原子的结合能最大。铁聚变要吸收能量,这是做不到的。铁核会坍缩,也会进入电子简并态。但电子简并压力也抗衡不了引力,还会继续坍缩。坍缩的能量会被消耗掉,加速坍缩。当铁核内部坍缩到原子核与原子核之间紧挨在一起时,坍缩终止,外部仍然在坍缩,就会撞击在内核上反弹。中微子会造成一个气泡,和反弹共同,形成向外的激波。这个激波就造成超新星爆炸。爆炸产生膨胀的尘埃气体云,核以中子星(中子简并压维持)的形式遗留,如果质量再大,连中子简并压力都不足以对抗引力,就会变成黑洞。
以这种原理产生的超新星爆炸根据恒星质量从小到大分为 II 型、Ib 型、Ic 型,这个是根据观测到的光谱分的,而光谱取决于外层的氢和氦是否已经被剥离。II 型有 H,Ib 型有 He,Ic 型没 He。
致密星
白矮星:由 $<8\sim 9M_\odot$ 的恒星演化而来(例如太阳最后会变成 $\sim 0.5M_\odot$ 的白矮星),半径跟地球差不多,因此密度很高,自转周期也很短。在同一温度下,白矮星的质量越小,半径越大,光度越高。具体来说,$R\propto M^{-1/3}$。同一白矮星半径不会显著变化。球状星团中的白矮星多。
中子星:超过钱德拉塞卡极限后,不断坍缩,电子速度会接近光速,质子和电子结合“逆衰变”为中子。原子核瓦解,整个星体变为中子海洋,中子简并压力抗衡引力。半径只有几十公里,密度比白矮星大很多,表面温度在刚形成时很高(但会很快耗散)。自转周期是毫秒级。根据广义相对论,中子星上的时间比地球慢(中子星表面已经有很明显的相对论效应了)。同样,中子星质量越大,半径越小,它的质量极限称为奥本海默极限,不确定,$\sim 3M_\odot$。
中子星的类别:
- 脉冲星(注意与脉冲变星区分!)。一些中子星会在磁轴发射电磁波,而磁轴与自转轴不共线,所以如果从地球能观测到,那周期就是中子星的自转周期。脉冲周期很稳定。
- 磁陀星。就是磁场很强的中子星。快速射电暴可能来源于它。
- 一般的中子星。
- 夸克星。质量较大的中子星,核心处夸克都变成自由的了。是一种假说的中子星。
虽说中子星在形成时表面温度很高,但半径太小了,没法借助黑体辐射观测。发现中子星的方式是观察周期性变化的电磁波,也就是“脉冲”。
黑洞:由质量 $>\sim 20M_\odot$ 的恒星演化而来。任何力都不足以抵抗引力,另一个表述是,表面的逃逸速度超过光速,即 $\sqrt{2GM/R}>c$。这个式子如果以 $R$ 作为未知数,得到 $R=2GM/c^2$ 称为引力半径或史瓦西半径。黑洞只有质量、角动量和电荷三个量,这称为黑洞无(三)毛定理。黑洞的平均密度 $$ \rho=\frac{M}{\frac43\pi R^3}=\frac{M}{\frac43\pi\frac{8G^3M^3}{c^6}}=\frac{3c^6}{32\pi G^3M^2} $$ 这个结果和白矮星、中子星的“质量越大半径越小”是反的,因为黑洞没法再坍缩了。当然实际上黑洞的所有质量集中在奇点。
黑洞分为史瓦西黑洞(不旋转,不带电)、R–N 黑洞(不旋转,带电)、克尔黑洞(旋转,不带电)、克尔—纽曼黑洞(旋转,带电)。
黑洞附近的光会被弯曲。黑洞的视界是指光能否逃逸的分界。对于史瓦西黑洞,引力半径等于视界半径;克尔黑洞有外视界和静界两个界,两者之间是能层,在能层不能保持静止,但可以逃离黑洞。黑洞的视界是单向的,在内部的事件无法对外部产生影响,在内部的时间对外部来说是静止的,视界处引力红移无限大,在内部的东西无法到外部来(尽管逃逸速度是指中途不加速的最大初速度,但即使在视界内向外走有燃料也是走不出来的,具体原因要用广相解释,科普文章)。黑洞的潮汐力会将进入它的物体撕碎。质量越大,视界处潮汐力越小。
克尔黑洞看起来很有意思。
如果太阳系的某个天体突然变成黑洞,它只会对附近的物质产生影响,质量不变,可以认为它是等效于原来的天体的。
致密星的演化
如果是单个孤立的致密星,白矮星和中子星会逐渐冷却(需要极长时间,$138$ 亿年内还不足以使白矮星或中子星冷却到较低温度,目前已知白矮星最低 $3000\unit{K}$ 不到,中子星最低 $42000\unit{K}$ 不到),白矮星最终变为黑矮星。它们的简并态都会维持。
黑洞会有霍金辐射,具体原理我也不知道。辐射与质量成反比: $$ T=\frac{hc^3}{8\pi GkM} $$ 因此黑洞会慢慢蒸发,寿命与质量平方成正比。
双星系统的情况就很不一样,最后都会并合。两个白矮星、中子星、黑洞并合的时候都会释放引力波。
小质量双星的演化:洛希瓣是一个恒星引力影响范围的边界。双星中质量较大的,先离开主序阶段,在膨胀超过洛希瓣后,其物质会被另一个星吸收,使另一颗星演化加快。前者最终变成白矮星,另一颗星随后膨胀,就反过来吸。这一吸的过程主要是氢下落到白矮星(仍有角动量)的吸积盘,同时引力势能转化为热能(数十万 $\text{K}$),发出以紫外波段为主的辐射,这个叫激变变星。在吸积的过程中,氢一直在白矮星的表面堆积,实际上因为白矮星是简并态,所以它反而会收缩,所以温度越来越高。当温度足以使氢核聚变时,会突然爆发,造成新星。多次新星称为再发新星。新星现象不会摧毁白矮星,反而会使白矮星质量增加。当白矮星的质量接近 $1.4M_\odot$ 时才会摧毁,这个称为 Ia 型超新星爆炸。
钱德拉塞卡极限:当白矮星质量增加时,电子简并压力增加(受相对论效应影响,$\propto M^{4/3}$)比引力增加($\propto M^2$)慢。超过这个极限,无论怎样坍缩,电子简并压力都无法克服引力。
关于 Ia 型超新星爆炸的细节:其本质是在接近钱德拉塞卡极限时,温度升高足以使碳核聚变,然后发生失控核聚变,整个炸掉。实际上这个质量会在 $1.38M_\odot$(不同类型的白矮星略有不同)。不可能出现达到钱德拉塞卡极限然后温和地坍缩成中子星。Ia 型超新星爆炸不会留下任何核心,只剩下超新星遗迹。中子星和黑洞只能通过其他几种超新星爆炸产生。
如果吸积不足以使这颗白矮星爆炸,就会剩下白矮星双星。它们互相公转会辐射(可观量的)引力波,角动量减小,最后会合并,同样产生 Ia 型爆炸(如果和小于 $1.4M_\odot$ 就合并成一颗白矮星)。
由于 Ia 型爆炸的光度一般都比较固定,所以也能当标准烛光。
宇宙中的铁主要来自 Ia 型爆炸。
超新星的命名是 SN + 年份 + 字母编号(同 Excel 列)。
超新星爆炸的主要能量释放途径是中微子。
超新星爆发所抛出的大量物质在向外运动膨胀过程中与星际物质和磁场相互作用而形成的气体星云,形成超新星遗迹(注意与行星状星云区分),是包括 X 射线在内的高能辐射源,这就是宇宙射线的起源。
许多中子星也都不是孤立的。中子星双星通过脉冲周期的周期性变化发现,同样双星也会释放引力波,逐渐靠近,最后合并,一般都会成为黑洞。
黑洞有两类,X 射线双星系统中的恒星级质量黑洞和星系中心的超大质量黑洞。
中子星和黑洞的转轴方向都有喷流,是由弯曲的磁场导致的。这个喷流叫相对论喷流,因为速度很快。不同级别的黑洞喷流的长度级别也不一样。
寻找恒星级黑洞,一般是寻找 X 射线双星。X 射线是怎么产生的呢?伴星的物质被黑洞吸积时,引力势能转化为内能,可以达到百万 $\text{K}$,发出的黑体辐射是 X 射线波段的。辐射的功率为 $$ L=\frac{GM\dot M}{r}=\eta\dot Mc^2,\,\eta=\frac{GM}{rc^2} $$ 其实很简单,就是引力势能的表达式(从伴星吸积的那个 $1/R$ 忽略),$M$ 表示黑洞的质量,$\dot{M}$ 表示吸积的质量效率,$r$ 表示吸积盘到中心的距离。化成后面这个式子就是为了长得像质能方程。$\eta$ 称为能量转换效率。代入史瓦西半径,黑洞的 $\eta<50\%$。
黑洞的发出的 X 射线是快速变化的(没仔细讲,我猜就是一下子吸了一堆?),因此如果观测到 X 射线峰,可以通过其时长推得黑洞的半径上限(近地球的一侧和垂直侧的距离(远地球一侧会被遮住),就是时长乘光速)。同时通过分析视向速度曲线可以得到质量。那么这样就可以确定是否是黑洞及其属性。典型例子:天鹅座 X-1。
黑洞是宇宙中最亮的。
伽马射线暴:短时间观测到大量伽马射线。产生机制是大质量恒星坍缩为中子星或黑洞(长爆),或者中子星与中子星、中子星与黑洞合并(短爆)。双黑洞合并不产生。喷流的物质与喷流的物质相撞产生的内部激波是伽马射线,而喷流的物质与星际物质相撞产生的外部激波,和超新星遗迹一样,产生的是 X 射线及以下的辐射。
如果较近的伽马射线暴的喷流指向地球,会有相对论聚束效应,对地球产生较大影响。
伽马射线暴和引力波的同时被观测验证了合并现象。
星团与星系
疏散星团年轻,球状星团年老,原因可以简单理解为,疏散星团引力不强,容易散开。如何得到一个星团的寿命?看这个星团的赫罗图上恰好进入或离开主序带的星,根据寿命与光度的关系推。
银河系
银河系的结构
因为太阳系处在银河系之中,所以银河系本身的结构难以以可见光观测得到(有星际消光)。漩涡结构是通过中性氢 21 厘米射电辐射观测到的,棒旋星系结构是通过红外波段观测。

这是银河系的结构,主要有几个部分:
- 银心 & 核球。银心有个超大质量黑洞,核球处恒星密度很高。
- 银盘。俯视来看,银盘分为数条旋臂,最大的四条为英仙臂、人马臂、猎户臂、天鹅臂。平视来看,有薄盘和厚盘。薄盘的恒星密度更高。
- 银晕。从内到外分为内晕、外晕和热气体云。
- 星团。疏散星团主要分布在银盘内,球状星团主要分布在银晕内,数量较少。
- 银河系中还有大量暗物质。通过观测中性氢的射电的多普勒效应,分析距离银河系中心不同距离处的公转速率(自转曲线),可以得到质量分布。如果只考虑中心天体作为引力源,应该有 $v\propto r^{-1/2}$。但是银河系不太靠中心的部分速度并不随着距离增加而减小,而是速度曲线相对平直,这个称为“较差自转”(我们上面在太阳中物质的转动中也提到过这个概念),我们可以据此预测质量分布。但预测的质量分布与实际的亮物质的分布不符,所以科学家预言暗物质的存在。暗物质主要分布于太阳轨道以外的区域,主导着银河系的总质量,其范围远超亮物质的范围。
- 但是如果只考虑较差自转,按说旋臂会消失。解释旋臂图案稳定的理论是密度波理论。旋臂并不是大量物质驻留的地方,而是物质密度高的地方(物质一直在移动,类比车流)。旋臂是少量的年轻的大质量、高光度、炽热恒星聚集的表现。
- 银河系中心有个大质量黑洞,且恒星聚集。通过高分辨率望远镜观测银心附近的恒星轨道,可以推算黑洞的质量。也偶有观测到中心的黑洞的 X 射线暴——潮汐瓦解事件。偶有,说明黑洞不太活跃。发现的银河系伽马射线泡说明以前黑洞是活跃的。
银河系中的恒星
这里提一下星族的定义:I 是含金属丰富的恒星(如太阳),II 是金属很少的恒星(如第二代恒星),III 是不含金属的恒星(第一代恒星)。
银河系中的恒星分为:
- 盘族恒星(I),在银盘面中环绕银心转动,比如太阳。相对年轻。
- 晕族恒星(II),轨道面方向任意。相对年老。一些晕族恒星的轨道穿越太阳附近的银盘。
- 棒族恒星(II)。
上面我们提到了,大爆炸只产生了氢、氦、锂,而重元素是通过红巨星、红超巨星、超新星爆炸、中子星合并产生的。所以我们说,重元素丰度随星际介质和恒星间的循环而增加,一颗恒星中重元素的丰度和其诞生时间是正相关的。于是可以通过分析恒星的光谱知道它的年龄。科学家希望找到含重元素很少很少(甚至没有)的恒星,就是宇宙早期形成的恒星。
银河系的恒星的年龄分布:
- 银晕和核球外层的恒星年老。银晕和核球外层气体含量较少,这些地方恒星形成早已停止。尽管年老,但仍有较少的重元素,并非第一代恒星。
- 银盘和核球内层的恒星相对年轻。核球内层气体密度很高,性质与银盘类似,恒星还在一代代持续形成。从银盘内区到外区,气体密度逐渐降低,恒星形成率逐渐降低,重元素丰度逐渐降低。
- 形成银盘及其恒星的气体,之前已经历显著的恒星形成。
本星系群
本星系群中主要的星系有:仙女座星系 M31(质量最大,旋涡)、银河系、三角座星系 M33、大小麦哲伦星云(矮星系,其中恒星正在形成)、还有一堆其他的矮星系环绕着主要的星系(像卫星一样,也成为伴星系)。推测:一个巨大的暗物质团块中的气体坍缩成许多原星系。一些原星系并合成为银河系和仙女星系,其他就是矮星系。
通过比较不同距离(不同年龄)星系的大小、形态、黑洞质量,可以推测星系的并合历史。通过年老恒星可以推测,在并合成银河系之前,已经有恒星形成了。
银河系未来会与人马座矮星系发生次并合(不影响银河系结构),在之后会和仙女星系主并合(使得并合后变成巨椭圆星系)。
星系
星系是由引力束缚的,尘埃、气体、大量恒星组成的集合体。伽利略发现银河由众多恒星组成。以前由于观测能力限制,星系、星团、星云被统一认为成是星云,后来才区分。
梅西叶天体列表(1784)是 110 个经典的天体,包括两类星团、三类星云、星系。其中的天体命名就是 M + 序号,几个经典的要记的有:M1 蟹状星云、M31、M33、M42 猎户座大星云、M45 昴星团(它是疏散星团)。说到这里要巩固一下三类星云的定义区分:弥漫星云就是正常的星际尘埃与气体,就是相对密些罢了,主要成分是氢,可能未来会形成或正在形成恒星,能观测到它们是因为被附近(或其中)的恒星照亮。恒星状星云和超新星遗迹上面有提。
希望有一天也能自己拍这个列表。
后面:星云和星团总表(CN,1786)→ 星云和星团总表(GC,1864)→ 星云和星团新总表(NGC,1888)。所以后来就用 NGC + 序号了。
星系的哈勃分类
按照星系在可见光波段的形态分,没有星系演化的意义。
-
椭圆星系。看起来就是个放射渐变的椭圆形。按照扁率分为 E0~E7 共八类。具体来说, $$ E=10\left(1-\frac ab\right) $$ 其中 $a$ 是短轴长,$b$ 是长轴长,所以说越扁 $E$ 越大。椭球照理说有三个参数,但关于星系的转轴应该是旋转对称的,所以就只有两个。
也有一种分类是分巨椭圆星系和矮椭圆星系。
椭圆星系中的恒星多是年老的小质量恒星,且其不再产生恒星。颜色一般偏红。正常来说不会有尘埃带。
-
旋涡星系。中间一个核球,周围一个星系盘上有旋臂。分为 Sa、Sb、Sc 三类,按顺序核球变小,旋臂变松、展开。
棒旋星系。中间恒星聚集成棒状结构,穿过中心,延伸到星系盘。分为 SBa、SBb、SBc 三类,类似。
这两类星系有星系晕,主要包含年老的小质量恒星。星系盘上的恒星相对较年轻。星系盘上会有尘埃带(遮光)。核球和星系盘偏红,星系盘偏蓝。
透镜状星系分为 S0 和 SB0,可以理解为没有旋臂的旋涡/棒旋星系。是介于这两者与椭圆星系之间的一类。
-
不规则星系。无核球,无旋臂,无对称性,记作 Irr(也可以细分 Irr I、Irr II、dIrr),其中多年轻恒星且正在形成恒星。形成原因是被附近星系的引力扭曲。
几乎所有星系中心都有超大质量黑洞。(部分矮星系没有,例如麦哲伦)
恒星的运动决定星系形态,在椭圆星系以及旋涡/棒旋星系的核球中,恒星的运动方向随机,可能某个平面方向上速度较大些,整个看起来就是扁的。
银河系是 SBb/SBc,M31 是 SBb,M33 是 Sc,大小麦哲伦是 Irr。
星系中的暗物质
暗物质占星系总质量的 $\sim90\%$,范围也比亮物质大,称为暗物质晕。
旋涡星系的自转速度曲线需要暗物质,椭圆星系的热气体的存在需要暗物质(椭圆星系没法用测量转速来分析,因为其中的恒星轨道不在同一平面上。椭圆星系外围弥散着 X 射线,说明有温度很高的气体,从而知道这些气体的速率很大(why?热运动和正常运动应该是分开的呀),从而推得转速曲线,说明有额外的引力,也就是由暗物质产生)。
关于暗物质是什么,最主流的观点是 WIMPs。微引力透镜的观测否定了暗物质是 MACHOs 的说法。
活动星系核
二十世纪天文四大发现:类星体、脉冲星、宇宙微波背景辐射和星际有机分子。
类星体:非常远的(所以是在宇宙年轻时的),致密的亮射电源,从可见光波段来看,没法放到赫罗图上(因为光度太高了),而且光谱上都是发射线(一般的恒星射电辐射是很弱的,且恒星都是吸收线)通过哈勃红移可以得出(极远的)距离,得到光度极高。观测得到类星体有喷流。那么实际上类星体是星系的剧烈活动的核心——它是活动星系核的一种。
具有剧烈活动现象的星系称为活动星系,核心不活动的星系称为正常星系或宁静星系,比如银河系。活动星系的分类:
- 星爆星系,剧烈恒星形成。通常是两个星系合并时出现。
- 活动星系核(AGN),就是中心的大质量黑洞在不断吸物质。活动星系核有高光度、光谱有发射线、快速光变、辐射波段广、高偏振等特点。具体来说,根据辐射在各波段的特征,它具体又分为:
- 类星体。细分为射电噪的和射电宁静的。类星体和其他情况的一个不同点是,它必须要距离很远,或者说红移很大。
- 赛弗特星系。注意这个并不是某个特定星系的名称!这个是射电宁静的一类,处于旋涡星系或不规则星系的中心。
- 射电星系。处于椭圆星系中。有明显的射电瓣。
- 耀变体。能量很高,光度很大,射电噪的。
更加精确地分析活动星系核,我们从光度和结构来说:
AGN 的能量来自太阳系大小的区域。这里有个考点是根据光变时标算尺寸:假设黑洞吸积了一堆物质,吸积盘突然发光,那么如果地球在盘所在平面,那么从地球观测到的辐射峰的时长,就是吸积盘的宽度除以光速。当然这个算出的只是一个很松的上限。
同时 AGN 有非常长直的相对论性喷流,可以达到数千万光年。
在这么一个小区域内能产生千亿倍太阳光度的辐射,它的辐射压就很大,一定有很大的自引力,也就是很大的质量,才能维持它的稳定。爱丁顿光度 $L_{\text{edd}}\propto M$ 表示对应质量的恒星的最大光度(同时可以推出不存在质量大于约 $100$ 倍太阳质量的恒星)。那么根据测得的数据,可以确定黑洞的质量下限。
对于不活跃的黑洞,它吸积的效率是很低的。根据光度和能量转换率可以算出,比如说 M87 中心黑洞一年大概吸积半个木星质量。
从结构上来说,活动星系核可以分为几部分:黑洞、吸积盘、喷流、宽线区、窄线区、尘埃环。宽窄线的意思就是观测到的光谱的发射线宽度不同,这个是因为产生发射线的被电离气体的速度范围不同,靠近中心而速度大的,因为多普勒效应就会使发射线展宽。
目前公认的说法是,不同种类的 AGN 是与观测夹角不同的,但同样性质的活跃黑洞。因为 AGN 的结构这么复杂,从不同角度看,可能会因为尘埃、和喷流的夹角、相对论效应等,得到很不同的观测结果:
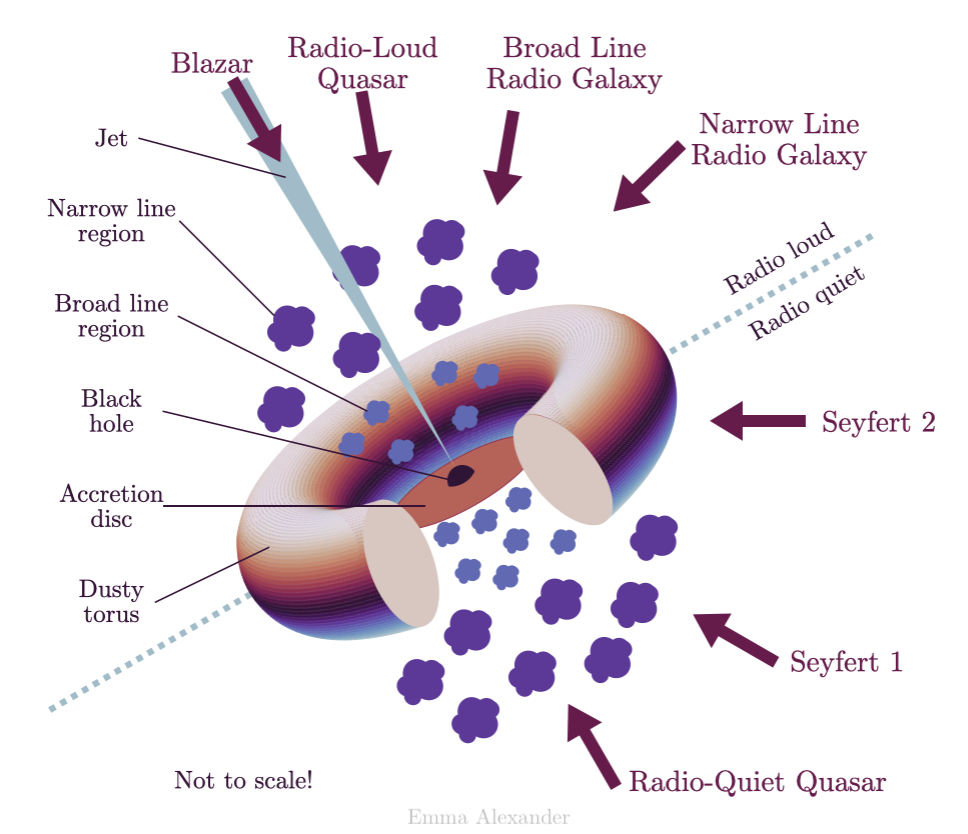
早期(遥远)星系中,AGN 比例要高很多。
蟹状星云可以作为标准烛光。
事件视界望远镜(EHT)拍到了 M87 中心的和人马座 A(银河系中心)黑洞,当一个星系确认黑洞后,其代号后面就会加上星号。
黑洞的质量测量方法就是观测中心附近的气体、恒星等的运动。
宇宙
宇宙的膨胀
历史:弗里德曼建立宇宙的数学模型,斯莱弗发现宇宙学红移,勒梅特提出大爆炸假说,哈勃发现退行速度与距离成正比。
宇宙不存在边界,可以类比吹气球的过程。
宇宙学原理:宇宙是处处一样的,物理定律处处使用。在大尺度上,宇宙是均匀的,各向同性的。宇宙任何地方的“观测者”都应看到相同的宇宙。这个可以通过观测验证——一方面是各个方向的恒星密度均匀,一个就是几乎所有星系都在远离我们。
接下来我们说的都是不考虑相对论效应的情况,因此不能处理速度太大,距离太远的情况。
那么既然宇宙是各向同性的,宇宙的膨胀也是各向同性的。这个性质用数学语言描述,就是相对于每个位置的观测者来说,都有 $$ \boldsymbol{v}=k(t)\boldsymbol{r} $$ 远离速度只与当前的时间与距离有关。
现在我们引入第二个假设,就是等速膨胀——宇宙膨胀速度是不变的(实际早期是减速膨胀的)。这句话的意思是说,取宇宙中的两个点,它们随着膨胀互相远离,远离的速度时时刻刻是一样的。用数学语言来说,假设两点的距离是 $d(t)$,那么 $$ \left\{\begin{aligned} d(t)&=\int_0^tv(t^\prime)\mathrm{d}t^\prime=\int_0^tk(t^\prime)d(t^\prime)\mathrm{d}t^\prime\\ k(t)d(t)&=C \end{aligned}\right. $$
从而 $d(t)=Ct$,$k(t)=1/t$。也就是说两个点之间的距离关于时间是正比例函数。这就是哈勃定律 $$ v_r=H_0d_G $$ $H_0$ 就是宇宙年龄的倒数。
现在我们考虑实际的问题:在观测到一个天体时,我们既不知道它的退行速度,也不知道它的距离,我们只知道它的光谱,可以通过比对几个关键谱线推出宇宙学红移 $z=\Delta\lambda/\lambda$。那么怎么推出现在它的距离呢?上课讲的是,直接用 $$ z=\frac vc,\,d=\frac v{H_0} $$ 来算。但是我们面对的毕竟是空间膨胀而不是简单的远离啊,$z=v/c$ 这事真对吗?所以我想仔细算一遍。
考虑它发射当前观测到的光时,距离地球 $d_0$,宇宙年龄 $t_0$。以它的发射点为数轴原点,在光以 $c$ 的速度正向移动的同时,空间在膨胀,设光所在位置为 $y$,单单膨胀带给它的速度为 $y/t$。两个速度叠加,得到 $y^\prime=c+y/t$。如果最终在 $t_1$ 时间到达地球,那么 $y|_{t=t_1}=d_0t_1/t_0$。
先解这个微分方程。齐次解为 $y=Ct$,非齐次解为 $y=ct\ln t+Ct$,代入初始条件得 $y=ct\ln(t/t_0)$。结合另一个方程解得 $t_1=t_0\mathrm{e}^{d_0/ct_0}$。光线到达地球的时候,红移为 $z=t_1/t_0-1$,距离就是 $d_0t_1/t_0$。
在假定距离不太大,也就是 $d_0/ct_0$ 不太大的情况下,可以用 $\mathrm{e}^x\approx 1+x$ 来估算:$t_1=t_0(1+d_0/ct_0)$,$z=d_0/ct_0$,$d_1=d_0t_1/t_0=zt_1=zct_1=zc/H_0$。嘿,它是对的。也就是说,我们可以通过观测以前发出的光来推断发光的天体现在的距离。
$z$ 很大的情况,就算用的是不估计的表达式,也会因为相对论问题出错。比如说在一个模型下(Friedmann 方程): $$ t=\frac1{H_0}\int_0^{1/(1+z)}\frac{\mathrm{d}a}{a\sqrt{0.3a^{-3}+0.7}} $$ 但无论如何有个东西还是对的,就是 $z=t_1/t_0-1$,或者说在这光发出的时候,宇宙尺度因子(现在是 $1$)是 $R_{\rm U}=1/(1+z)$。
那现在的问题就是测得哈勃常数 $H_0$。不能选太近的天体,不然本动速度(除去随着膨胀,相对于地球的速度)就会严重影响结果。但太远的本身就不知道距离,怎么办呢?这里有一个距离阶梯的方法:
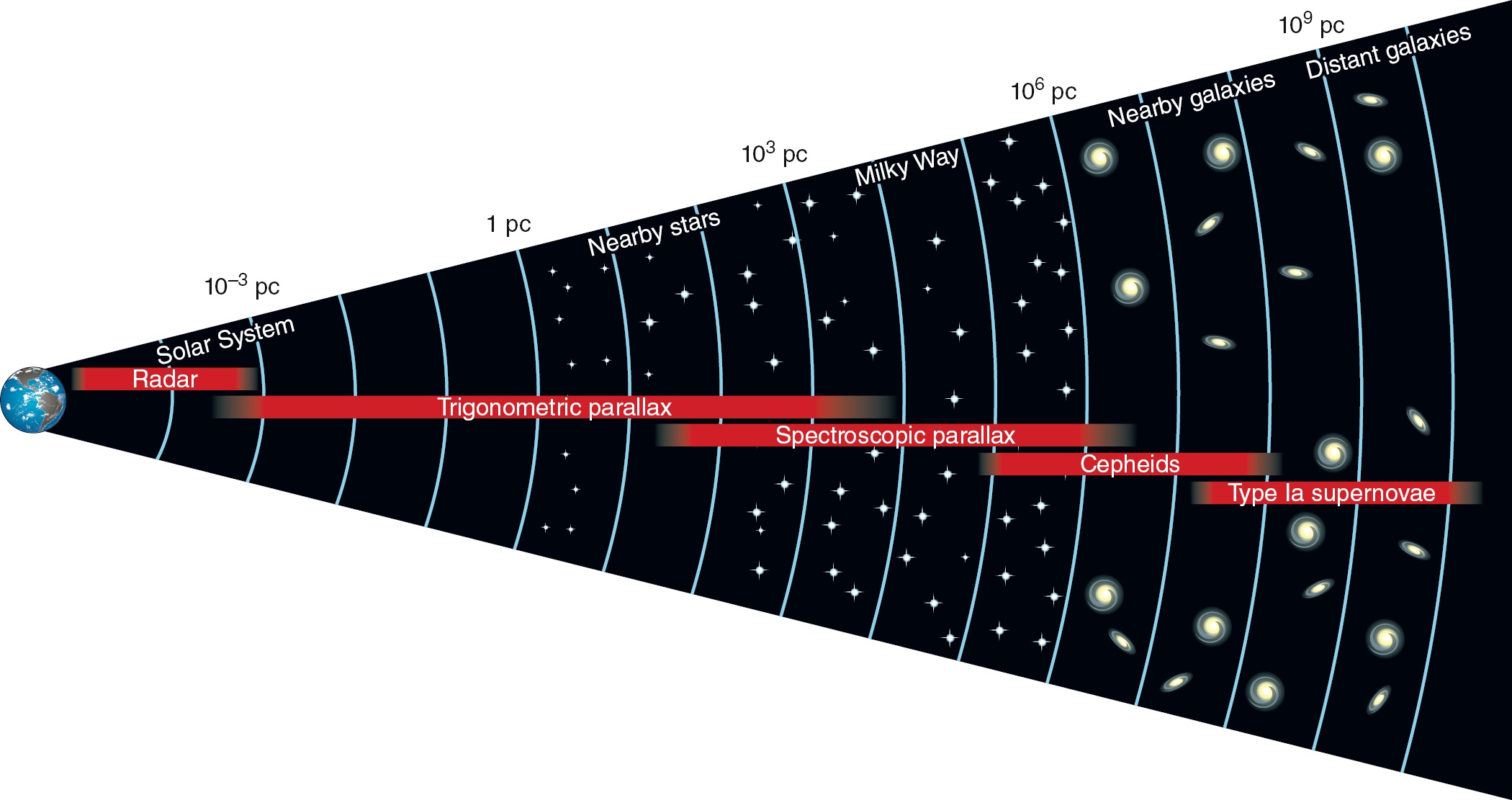
比如说,我们知道造父变星的光度,并发现有一个星系里既有造父变星,又有一个 Ia 超新星,那么就可以得到超新星的光度,从而往更远的推。哈勃当时用的标准烛光是造父变星,测得偏大了很多。
宇宙微波背景辐射
热大爆炸宇宙学模型:1948,伽莫夫,αβγ 论文。
宇宙大爆炸只合成了最轻的元素:氢、氦、锂(宇宙中锂铍硼的丰度很低是因为它们不是核聚变的产物,而是被核聚变消耗)。铁及之前的元素是通过大质量恒星的核聚变出现,比铁重的原子是通过中子俘获 + β 衰变形成,在例如超新星爆炸、中子星并合等事件中。
宇宙微波背景辐射(CMB)是宇宙大爆炸发生的重要证据。它是能看到的宇宙最早期的辐射。最早由上面的这篇论文预测,后来,1964、65 年由贝尔实验室的几位科学家偶然观测到(最早的好像是苏联的科学家)。
$38$ 万年之前的信息没法从电磁波角度了解,因为那个时候之前因为原子都被电离了,光子没法自由移动,或者说宇宙对电磁波是不透明的。在那之后,宇宙复合(中性化),温度约三千 $\rm K$。随着宇宙膨胀,温度继续下降。CMB 也随着从伽马射线波段(冷却)到红外波段,再(红移)到微波波段,现在宇宙的平均温度只有个位数 $\rm K$,总体来说,宇宙膨胀了 $1100$ 倍,温度下降了 $1100$ 倍,CMB 波长峰值红移了 $1100$ 倍。
CMB 的谱需要到太空中观测,COBE 观测得到,它极其完美地符合 $2.73\unit K$ 黑体辐射谱。
CMB 高度各向同性,但是从地球来看有轻微的不同性,因为地球相对于宇宙空间有一个速度,这就是 CMB 的偶极不对称性。当扣除这部分,以及其他微波辐射源、尘埃消光的影响,发现 CMB 在高度各项同性的基础上有十万分之几的各向异性。(这种各向异性很重要,因为它这种不均匀是形成各种天体的种子)

WMAP 探测器观察的角分辨率更高,把背景辐射的极差提高到了万分之二。后面还有 Planck。这些观测都进一步给出了更精确的哈勃常数以及宇宙中的物质分布比例。
大爆炸核合成的说法,解释了氦的观测得丰度高于恒星核合成的产量对应的预估。在大爆炸后的短时间内,质子碰撞合成轻原子核,这个叫大爆炸(原初)核合成。
通过数学预测的各元素比例和实测的各元素比例,可以得到宇宙的亮物质(重子)密度。
宇宙结构的起源
我们希望找到宇宙最早的天体发出来的光。
上面我们提到,星系的形成是因为引力,那么这个引力主要是暗物质。星系也会聚集起来形成星系群或星系团(星系群里星系少,星系团里星系多)。总体来说,矮星系数量远多于巨星系,旋涡星系常见。少部分星系团中,椭圆星系(主要由旋涡星系并合而成)主导。本星系群(银河系、M31、M33、大小麦哲伦)的周围有室女星系团(中心 M87)、后发星系团等,都是形如中心一个椭圆星系,周围一堆旋涡星系。本星系群和室女星系团都(不含后发)属于室女(本)超星系团,中心在室女星系团附近。
绘制宇宙的大尺度结构,就用哈勃红移算距离。星系不是随机分布,而是组成复杂的网状结构。由星系组成的纤维和“墙”环绕着巨洞。像海绵或者说泡泡的结构。
暗物质也主导星系团、群的质量。测的方法跟星系内是一样的(看各星系速度、看炽热气体的 X 射线、引力透镜)。星系团的暗物质先于星系的暗物质被提出。
宇宙一开始是非常均匀的,其极其微小的“微扰”不均匀性是形成现在复杂星系结构的原因,有个蝴蝶效应在里面。大爆炸后 $38$ 万年到数亿年期间,没有恒星(正在形成),这段时期称为黑暗时期。这段时期的研究是靠观测中性氢的 $21$ 厘米辐射。
宇宙暴胀时期的量子涨落产生了密度涨落,为星系和星系组合提供了“团块(种子)”,引力不稳定性把宇宙的密度涨落转变为星系。CMB 各项异性是量子涨落的印记。目前的说法是,形成的过程是自下而上等级式成团:小结构先形成,再形成大结构。
大爆炸宇宙学的标准模型是 ΛCDM 模型,可以通过计算机模拟来研究。它有四个参数:暗能量(Λ)、(冷)暗物质(CDM)、亮物质、哈勃常数。这些参数取不同的值,宇宙的演化情况是不同的,只有特定的参数组合才能导致现在宇宙的大尺度结构。但是无论如何,初始情况不能绝对均匀,得有形成结构的种子,这就靠 CMB 的观测数据得出。亮、暗物质开始于等同的密度涨落(也等同于 CMB),但 $38$ 万年后,亮物质受到辐射压的影响,模糊的程度强于暗物质(暗物质不与辐射互动)。暗物质分冷暗物质(未知基本粒子,质量大、运动慢)和热暗物质(粒子质量轻、运动极快)。热、冷暗物质共同形成最大尺度的结构,冷暗物质形成星系尺度的结构。冷暗物质和亮物质一起坍缩,冷暗物质为亮物质提供引力。当坍缩到一定程度时,暗物质因为无法发出辐射,引力和辐射压就平衡了,无法坍缩,亮物质可以通过辐射失去热量,而逐渐变小。这就是为什么亮物质形成小而扁的星系,而暗物质弥漫在大得多的范围。
黑暗时期过后($5.5$ 亿年),第一代恒星开始在在暗物质微晕中形成,原初气体云在一小部分中性氢形成分子氢、冷却气体云后,因压力降低而引力坍缩。因为开始的时候,无重元素,无尘埃,无冷而致密的分子云,只有氢和氦,它们的能级少,不容易通过辐射散热,所以气体云必须足够大才能坍缩,所以就没法形成小质量的恒星。这些大质量的恒星,辐射紫外线,电离周围的气体。它们寿命短,经历超新星爆炸后,结局都是 X 射线双星,黑洞。甚至可能从气体云直接坍缩成黑洞。有说法说,并合的恒星质量黑洞成为星系中心超大质量黑洞的种子。
第二代有了重元素(当然还是丰度很低),就跟现在差不多了。第二代恒星提供关于第一代恒星的性质与银河系早期的物理条件的线索。根据上面说的自下而上的形成顺序,第一代矮星系和第二代恒星同时形成,其中有些小质量恒星现在仍处于主序阶段,这些在第二轮中首次出现的小质量恒星称为第一代小质量恒星。本星系群里也有大量这个时候形成的超弱矮星系,光度很低,暗物质比例很高,极低金属丰度。在第二代恒星形成后,可能没有再形成恒星。是第一代星系的化石。还有球状星团,球状星团相比矮星系,其中的暗物质密度更低,大小也小。
早期宇宙更小、星体数量更多、星体更靠近,所以并合更频繁。在大的旋涡星系附近,存在大量矮椭球星系与球状星团,它们可能是大星系由小星系并合而来的证据。越早期的星系,越暗弱、混乱、形状不规则。
超大质量黑洞的质量与旋涡星系的核球和椭圆星系(整个椭圆星系就可以视为核球)的质量正相关。星系(黑洞)在并合时会触发恒星形成区。恒星形成率在宇宙 $20$ 到 $30$ 亿年时最高。
两个星系团碰撞时,恒星和暗物质不改变,热气体会减速。
韦布望远镜发现,早期星系中规则的星系数量远多于标准模型所预言的。
宇宙的未来与极早期
实际上宇宙不是等速膨胀的。
在没有暗能量的概念时,科学家认为,因为宇宙有质量,就有引力,所以膨胀一定时减速的。那么具体的减速情况就取决于宇宙本身的“逃逸速度”。假设现在宇宙的平均密度为 $\rho$,有个距离地球 $d$ 的天体,它以 $H_0d$ 的速度远离。它所受的指向地球的引力,可以视作半径为 $d$ 的球里面的物质的引力,质量为 $\frac43\pi d^3\rho$。那么逃逸速度为 $$ \sqrt{\frac{2GM}d}=\sqrt{\frac{8\pi Gd^2\rho}3} $$ 能够逃逸的临界情况为 $$ H_0d=\sqrt{\frac{8\pi Gd^2\rho}3}\Longrightarrow\rho=\frac{3H_0^2}{8\pi G} $$ 与 $d$ 无关。也就是说,如果 $\rho$ 小于等于这个值,宇宙就能一直减速膨胀下去,否则最后就会宇宙大收缩。这个临界值称为宇宙的临界密度 $\rho_{\rm c}$。宇宙的物质密度参数定义为 $$ \Omega_{\rm mass}=\frac\rho{\rho_{\rm c}} $$ 其中 $\rho$ 为观测得到的密度。如果 $\Omega_{\rm mass}\le 1$ 就会一直膨胀。实际测得它约为 $0.32$。
如果宇宙真的是减速膨胀的,那我们通过标准烛光法(实际)和哈勃定律(假定是匀速膨胀)得出来的某个遥远天体的距离会怎样不同呢?
首先明确标准烛光法测得的是当前的距离而不是发光时的距离,设为 $d$。我们认为 $H_0$ 取的是真实测得的,当前宇宙的膨胀速度比例。设 $z$ 为测得的红移。那么发光时天体与地球的距离比当前的距离就是 $1/(1+z)$,这个前面提过。那就是说,从 $d/(1+z)$ 到 $d$,是通过一个减加速(上凸)的过程,光刚好能传到地球。如果我们用匀速的方法(即 $zc/H_0$)来测,那么就不可能是从 $d/(1+z)$ 到 $d$,因为在匀速的情况下,光因膨胀而“吃到”的减速没有那么多,所以在膨胀到 $d$ 之前就已经到达了地球,这就不对了。解决这个的方法就是增大 $d$。所以匀速模型下测得的结果,如果要自洽,就是距离偏大。
这个东西老师上课没仔细讲,然后实际上你简单想想很容易觉得,它不应该是减速模型距离偏大吗?这个东西实际上还真没这么简单,你仔细分析,实际上考虑的是这么一个问题:对于微分方程 $$ y^\prime=c+\frac{a^\prime(t)}{a(t)}y $$ ($a$ 就是尺度因子),其中 $a(0)=1/(1+z)$,$a(t_0)=1$,$y|_{t=0}=0$。考虑方程 $$ y=a(t)d_0 $$ 的解 $t_1$,那么当 $a(t)$ 是一次函数时,这个解一定比 $a(t)$ 是上凸函数时的解小。可以得到解为 $$ y=a(t)\cdot c\int_0^t\frac{\mathrm{d}u}{a(u)} $$ 因此等式相当于 $$ \int_0^{t_1}\frac{\mathrm{d}u}{a(u)}=\frac{d_0}c $$ 肯定是一次函数累积得最快。
如果你有更简单的解释请留言。
哎呀反正考试的时候记得是减速偏小就行啦。
那么实际结果观测结果恰恰相反。这说明宇宙中有一个斥力。爱因斯坦在用广义相对论预言宇宙发展时,为了符合他认为的宇宙稳定,加入了起长程斥力的宇宙学常数 $\Lambda$。现在这个量反而可以用来对应斥力了。这个斥力是由暗能量造成的。暗能量均匀分布,不聚集成团,仅在巨大时空尺度上起作用。同样有一个暗能量密度 $\Omega_\Lambda$。暗能量在宇宙早期不重要,在约一半宇宙年龄前宇宙膨胀是减速的。随着宇宙膨胀,引力越来越弱,暗能量(密度不变)占主导,使减速转为加速。但暗能量具体是什么还不知道。宇宙的膨胀模式是物质和暗能量(时间演化)共同作用的结果。
如果宇宙膨胀减速,则宇宙年龄 $<1/H_0$;宇宙膨胀加速,则宇宙年龄 $>1/H_0$。
宇宙的总密度参数 $\Omega_0=\Omega_{\rm mass}+\Omega_\Lambda$ 决定宇宙的形状,它是等于 $1$ 的,这意味着宇宙是平直的。
关于早期宇宙,就几个知识点:
粒子的创建需要很高的温度。产生:两个伽马射线光子碰撞,产生正反粒子对。湮灭:粒子与反粒子对湮灭, 质量转为能量。辐射场温度越高,所创建的粒子的质量越大。在阈值温度之上,粒子—反粒子对和辐射处于热平衡状态,即对产生和对湮灭平衡;在阈值温度之下,对湮灭之后粒子不能再被创建。宇宙年龄 $\sim 0.0001\unit s$ 后,质子不再创生。宇宙年龄 $\sim 100\unit s$ 后,电子不再创生。物质略微超过反物,每十亿个粒子—反粒子对,多出一个额外的粒子。随着宇宙膨胀冷却,对湮灭后对产生不再发生,这些幸存的没有配对的正粒子从辐射场中冻结出来,其数量一直恒定至今。
后面是宇宙初期演化的八个时代,然后平直疑难问题、视界疑难问题、宇宙的结局。
宇宙的未来有两个说法,大撕裂和热寂。
雨课堂测试的几个知识点
- 金星的盈亏(越亮越小,伽利略发现)彻底否定了地心说。
- 伽利略是通过造父变星测距而得到星云不属于银河系的,因为他没有区分 I 型和 II 型,所以测得 $H_0$ 误差大。
- 空间望远镜的最大不利因素是昂贵。
- 地球表面不能探测 X、γ 射线。
- 目前最常用的发现系外行星的方法是凌星法。
- 天狼星的白矮星伴星是通过天体测量法发现的。
- 双黑洞的并合不产生 γ 射线暴,只有大质量恒星坍缩,或者合并中有至少一者为中子星才能。
- 年轻恒星主要位于银河系的旋臂,而不能说银盘。
- 哈勃确定(旋涡)星云是银河系外的星系的关键是,他(利用造父变星)测量出了其距离。
考试的一些知识点
这边列出的是一些我不太清楚的或者觉得相对容易忽视的。您需要先保证复习完主要的知识点和雨课堂测试题。每届的题目肯定是不一样的。
- 中国农民丰收节的时间是秋分。
- 冬季大三角。
- 狭义相对论效应能解释 μ 介子。
- 变星的周光关系与多普勒效应无关,其他很多天体的发现都和多普勒有关。
- 双射电脉冲星一定是两颗中子星。两颗中子星合并后不一定是黑洞。发现第一颗双射电脉冲星获诺贝尔奖。
- 太阳表面的震荡可以体现内部结构。
- 太阳具有 $22$ 年的磁周期。
- B-V 值的严格定义——峰值波长越短,B-V 越小。
- 太阳是 G2V 型。
- 黑暗时期靠中性氢研究。
- 活动星系核不包含恒星。
- 行星状星云是由气体被电离所致。
- 球状星团中暗物质比例较小。
- 原太阳与太阳比,光度、大小、颜色中,颜色差的相对来说最小。
- 疏散星团几乎没有白矮星,球状星团里有很多。
- 天琴 RR 主要在银河系内被观测到,造父变星则相反。
- 白矮星 Ia 爆发有两种:经典是吸积到钱德拉塞卡极限,超亮是两颗白矮星并合。我不知道为啥试卷里是单选。
- 通过两个星团中正在离开主序带的恒星的年龄等,比较星团的年龄。
- 人马座 A* 黑洞就是银河系中心。
- 大爆炸核合成预言了今天宇宙的轻元素丰度。
- 两个星系高速碰撞时,亮物质热气体减速,暗物质不减速。
- 暴胀期解释了视界问题。
附录
课内公式
$r$ 和 $R$ 均表示半径,$m$ 和 $M$ 均表示质量。
太阳日和恒星日的差: $$ 太阳日-恒星日=恒星日\times\frac{太阳日}{恒星年}\approx\frac{24\unit{h}}{365} $$ 某地 $x$ 日(从春分日起)$y$ 时的地方恒星时: $$ \left(x\times 4\unit{min}+y-12\unit{h}+\frac{该地经度-该地时区中央子午线}{360^\circ}\cdot 24\unit{h}\right)\bmod 24\unit{h} $$ 向心加速度: $$ a=\frac{v^2}{r}=v\omega=\omega^2r=\frac{4\pi^2r}{T^2}=4\pi^2f^2r $$ 万有引力: $$ F=\frac{Gm_1m_2}{r^2} $$
黄金代换: $$ GM=v^2r=gr^2 $$ 宇宙速度: $$ v_1=\sqrt{gR},\,v_2=\sqrt{2gR} $$ 开普勒第三定律: $$ \frac{a^3}{T^2}=\frac{GM}{4\pi^2} $$ 双星系统: $$ \frac{(r_1+r_2)^3}{T^2}=\frac{G(m_1+m_2)}{4\pi^2} $$
$$ r_1m_1=r_2m_2 $$
潮汐加速度($r$ 是受力星球的半径): $$ a=\frac{2GMr}{d^3} $$ 波: $$ E=hf $$
$$ \lambda f=c $$
红移($v$ 是视向靠近速度): $$ z=\frac{\Delta\lambda}{\lambda}=\frac vc $$ 黑体辐射定律(光谱辐射亮度): $$ B_\nu(\nu,T)=\frac{2h\nu^3}{c^2}\frac{1}{\mathrm{e}^{h\nu/k_BT}-1} $$ 峰值波长与温度的关系: $$ T=\frac{2.9\times 10^6\unit{nm\cdot K}}{\lambda_{\text{peak}}} $$ 流强: $$ F=\sigma T^4 $$ 光度: $$ L=4\pi R^2F $$ 亮度: $$ B=\frac{L}{4\pi d^2}=\frac{r^2}{d^2}\sigma T^4 $$ 凌星亮度下降率(假设恒星是朗伯辐射体): $$ p=\frac{R^2_{\text{planet}}}{R^2_{\text{star}}} $$ 聚光能力($D$ 是光圈大小): $$ A=\frac{\pi D^2}{4} $$ 角分辨率: $$ \theta=2.06\times10^5\frac\lambda D\unit{arcsec} $$ 角动量: $$ L=\iiint(\boldsymbol{r}\times\boldsymbol{v})\mathrm{d}m $$ 均匀球体的角动量: $$ L=\frac{4\pi mR^2}{5T} $$ 太阳核聚变的能量: $$ \Delta E=\Delta mc^2 $$ 距离与视差的关系: $$ d=\frac1p $$ 视星等: $$ m=-2.5\log_{10}\frac{b}{b_0} $$ 绝对星等: $$ M=-2.5\log_{10}\frac{L}{4\pi(10\unit{parsec})^2b_0} $$ 距离模数: $$ \mu=m-M=5\log_{10}d-5 $$ 色指数: $$ B\text{-}\!V=-2.5\log_{10}\frac{b_B}{b_V} $$
质寿关系(类日): $$ \tau_{\text{MS}}=10^{10}\unit{y}\cdot\frac{M/M_\odot}{L/L_\odot} $$ 史瓦西半径: $$ r=\frac{2GM}{c^2} $$ 黑洞平均密度: $$ \rho=\frac{3c^6}{32\pi G^3M^2} $$ 黑洞的能量转换效率: $$ \eta=\frac{GM}{rc^2} $$ 哈勃定律: $$ v_r=H_0d_G $$ 宇宙的临界密度: $$ \rho=\frac{3H_0^2}{8\pi G} $$
常数表
以下,秒分时日($\rm s,min,h,d$)均靠铯原子钟定义,平太阳日和 $1\unit{d}$ 差别极小。
部分数据取自 https://nssdc.gsfc.nasa.gov/planetary/factsheet/sunfact.html。
| 名称 | 符号 | 数值 |
|---|---|---|
| 光速 | $c$ | $2.9979\times 10^8\unit{m/s}$ |
| 天文单位 | $1\unit{AU}$ | $1.4960\times 10^8\unit{km}$ |
| 光年 | $1\unit{ly}$ | $9.4607\times 10^{15}\unit{m}$ |
| 恒星日 | $23.934\unit{h}$ | |
| 平太阳日 | $24\unit{h}$ | |
| 恒星年 | $365.256\unit{d}$ | |
| 太阳年 | $365.242\unit{d}$ | |
| 月亮公转周期 | $27.32\unit{d}$ | |
| 月相周期 | $29.53\unit{d}$ | |
| 目前地球自转轴进动周期 | $25772\unit{y}$ | |
| 万有引力常数 | $G$ | $6.6743\times 10^{-11}\unit{m^3/(kg\cdot s^2)}$ |
| 太阳质量 | $M_\odot$ | $1.9884\times 10^{30}\unit{kg}$ |
| 地球质量 | $M_\oplus$ | $5.9722\times 10^{24}\unit{kg}$ |
| 太阳半径 | $r_\odot$ | $6.957\times 10^5\unit{km}$ |
| 地球半径 | $r_\oplus$ | $6371\unit{km}$ |
| 光球层温度 | $5772\unit{K}$ | |
| 太阳光度 | $L_\odot$ | $3.828\times 10^{26}\unit{W}$ |
| 太阳赤道自转周期 | $25.05\unit{d}$ | |
| 第一宇宙速度 | $7.9\unit{km/s}$ | |
| 第二宇宙速度 | $11.2\unit{km/s}$ | |
| 普朗克常数 | $h$ | $6.6261\times 10^{-34}\unit{m^2\cdot kg/s}$ |
| 维恩位移定律的分子 | $2.8978\times 10^6\unit{\mu m\cdot K}$ | |
| 斯忒藩—玻耳兹曼常数 | $\sigma$ | $5.6704\times 10^{-8}\unit{W/(m^2\cdot K^4)}$ |
| 可见光波长范围 | $380\sim 750\unit{nm}$ | |
| 氢原子的电离能 | $13.598\unit{eV}$ | |
| 角分辨率的常数(课内) | $1\unit{rad}$ | $2.0626\times 10^5\unit{arcsec}$ |
| 角分辨率的常数(课外) | $1.2197$ | |
| 质子—质子链的能量转换效率 | $0.7\%$ | |
| 太阳寿命 | $\sim 10^{10}\unit{y}$ | |
| 秒差距 | $1\unit{pc}$ | $3.2616\unit{ly}$ |
| 钱德拉塞卡极限 | $1.4M_\odot$ | $2.765\times 10^{30}\unit{kg}$ |
| 银盘直径 | $26.8\pm 1.1\unit{kpc}$ | |
| 太阳距银心 | $8.32\pm 0.14\unit{kpc}$ | |
| 薄盘厚度 | $220\sim 450\unit{pc}$ | |
| 厚盘厚度 | $2.6\pm 0.5\unit{kpc}$ | |
| 哈勃常数 | $H_0$ | $70\unit{km/s/Mpc}$ |
| 宇宙年龄 | $1.38\times 10^{10}\unit{y}$ | |
| 宇宙背景辐射温度 | $2.72548\pm 0.00057\unit{k}$ | |
| 宇宙物质密度 | $3\times 10^{-27}\unit{kg/m^3}$ | |
| 宇宙临界密度 | $\rho_{\rm c}$ | $9.5\times 10^{27}\unit{kg/m^3}$ |
中英对照表
您甚至可以看术语来期末复习。
术语
| 中文 | 英文 |
|---|---|
| 天文单位 | astronomical unit |
| 光年 | light-year |
| 星座 | constellation |
| 极 | pole |
| 赤道 | equator |
| 北回归线 | the Tropic of Cancer |
| 南回归线 | the Tropic of Capricorn |
| 纬度 | latitude |
| 经度 | longitude |
| 子午线 | meridian |
| 本初子午线 | prime meridian |
| 天球 | celestial sphere |
| 天顶 | zenith |
| 地底 | nadir |
| 赤纬 | declination |
| 赤经 | right ascension |
| 黄道 | ecliptic |
| 地平(线) | horizon |
| 中天 | culmination |
| 过中天 | meridian transits |
| 高度角 | altitude |
| 方位角 | azimuth |
| 拱极星 | circumpolar star |
| 星轨 | star trail |
| 太阳日 | solar day |
| 恒星日 | sidereal day |
| 黄道带 | the zodiac |
| 自转 | rotate |
| 公转 | revolve |
| 春/秋分 | the spring(vernal)/autumn(autumnal) equinox |
| 夏/冬至 | the summer/winter solstice |
| 进动 | precession |
| 岁差 | precession of the equinoxes |
| 章动 | nutation |
| 月相 | phase of the moon |
| 新月 | new moon |
| 娥眉月 | waxing crescent |
| 上弦月 | first quarter |
| 上凸月 | waxing gibbous |
| 满月 | full moon |
| 下凸月 | waning gibbous |
| 下弦月 | last quarter |
| 残月 | waning crescent |
| 恒星年 | sidereal year |
| 回归年 | tropical year |
| 恒星周期 | sidereal period |
| 会合周期 | synodic period |
| 潮汐锁定 | tidal locking |
| 同步自转 | synchronous rotation |
| 日食 | solar eclipse |
| 日全食 | total solar eclipse |
| 日环食 | annular solar eclipse |
| 日偏食 | partial solar eclipse |
| 本影 | umbra |
| 半影 | penumbra |
| 地心 | geocentric |
| 本轮 | epicycle |
| 均轮 | deferent |
| 日心 | heliocentric |
| 顺行 | prograde motion |
| 逆行 | retrograde motion |
| 近日点 | perihelion |
| 远日点 | aphelion |
| 椭圆 | ellipse |
| 万有引力定律 | universal law of gravitation |
| 逃逸速度 | escape velocity |
| 潮汐隆起 | tidal bulge |
| 辐射 | radiation |
| 光谱 | spectrum |
| 紫外线 | ultraviolet radiation, UV |
| 红外线 | infrared radiation, IR |
| 光子 | photon |
| 质子 | proton |
| 中子 | neutron |
| 电子 | electron |
| 中微子 | neutrino |
| 发射线 | emission line |
| 吸收线 | absorption line |
| 红移 | redshift |
| 蓝移 | blueshift |
| 热辐射 | thermal radiation |
| 辐射强度 | radiant intensity |
| 流强 | flux |
| 光度 | luminosity |
| 亮度 | brightness |
| 光学望远镜 | optical telescope |
| 折射式望远镜 | refracting telescope |
| 反射式望远镜 | reflecting telescope |
| 物镜 | objective lens |
| 目镜 | eyepiece |
| 色差 | chromatic aberration |
| 色散 | dispersion |
| 立体角 | solid angle |
| 角分辨率 | angular resolution |
| 衍射极限 | diffraction limit |
| 视宁度 | seeing |
| 光谱仪 | spectrograph |
| 恒星 | star |
| 行星系 | planetary system |
| 卫星 | moon |
| 星云 | nebula |
| 流星 | meteor |
| 陨石 | meteorite |
| 原恒星 | protostar |
| 原行星盘 | protoplanetary disk |
| 角动量 | angular momentum |
| 吸积盘 | accretion disk |
| 双极流 | bipolar outflow |
| 喷流 | jet |
| 星子 | planetesimal |
| 行星迁移 | planet migration |
| 原始大气 | primary atmosphere |
| 次生大气 | secondary atmosphere |
| 彗星 | comet |
| 彗核 | comet nucleus |
| 类地行星 | terrestrial planet |
| 巨行星 | giant planet |
| 系外行星 | extrasolar planet/exoplanet |
| 矮行星 | dwarf planet |
| 褐矮星 | brown dwarf |
| 视向速度法 | radial-velocity method |
| 凌星法 | transit method |
| 微引力透镜法 | gravitational microlensing |
| 天体测量法 | astrometric method |
| 直接成像法 | direct imaging |
| 核合成 | nucleosynthesis |
| 核聚变 | nuclear fusion |
| 氢燃烧(氢核聚变) | hydrogen burning |
| (热)传导 | conduction |
| 对流 | convection |
| 不透明度 | opacity |
| 日面米粒组织 | granulation |
| 日震 | helioseismology |
| 光球层 | photosphere |
| 色球层 | chromosphere |
| 日冕 | corona |
| 临边昏暗 | limb darkening |
| 太阳黑子 | sunspot |
| 太阳黑子周期 | sunspot cycle |
| 太阳耀斑 | solar flare |
| 冕环 | coronal loop |
| 日珥 | solar prominence |
| 日冕物质抛射 | coronal mass ejection |
| 冕洞 | coronal hole |
| 太阳风 | solar wind |
| 极光 | aurora |
| 视差角 | parallactic angle |
| 视差 | parallax |
| 视星等 | apparent magnitude |
| 绝对星等 | absolute magnitude |
| 距离模数 | distance modulus |
| 色指数 | color index |
| 滤光片 | optical filter |
| 双星 | binary star |
| 质心 | center of mass |
| 视双星 | visual binary |
| 食双星 | eclipsing binary |
| 分光双星 | spectroscopic binary |
| 天体测量双星 | astrometric binary |
| 光谱型 | spectral type |
| 主序 | main sequence, MS |
| 巨星 | giant |
| 星际介质 | interstellar medium |
| 星际尘埃 | interstellar dust |
| 星际消光 | interstellar extinction |
| 红化 | reddening |
| 星际云 | interstellar cloud |
| 云际气体 | intercloud gas |
| 星云 | nebula |
| 电离 | ionize |
| 分子云 | molecular cloud |
| 巨分子云 | giant molecular cloud |
| 演化程 | evolutionary track |
| 星团 | star cluster |
| 球状星团 | globular cluster |
| 疏散星团 | open cluster |
| 褐矮星 | brown dwarf |
| 寿命 | lifetime |
| 质光关系 | mass-luminosity relation |
| 亚巨星(支) | subgiant (branch), SB |
| 红巨星(支) | red giant (branch), RGB |
| 简并 | degenerate |
| 氦闪 | helium flash |
| 水平支 | horizontal branch, HB |
| 渐近巨星支 | asymptotic giant branch, AGB |
| 后渐近巨星支 | post asymptotic giant branch, post-AGB |
| 行星状星云 | planetary nebula |
| 白矮星 | white dwarf |
| 黑矮星 | black dwarf |
| 不稳定带 | instability strip |
| 脉动变星 | pulsating variable stars |
| 造父变星 | Cepheid variable |
| 天琴座 RR 型变星 | RR Lyrae variable |
| 超新星 | supernova |
| 超新星遗迹 | supernova remnant |
| 中子星 | neutron star |
| 脉冲星 | pulsar |
| 黑洞 | black hole |
| 激变变星 | cataclysmic variable stars |
| 新星 | nova |
| 再发新星 | recurrent nova |
| X 射线双星 | X-ray binary |
| 主序转折点 | main-sequence turnoff |
| 磁星 | magnetar |
| 夸克(奇异)星 | quark star |
| 快速射电暴 | fast radio burst, FRB |
| 视界 | event horizon |
| 奇点 | singularity |
| 能层 | ergosphere |
| 相对论性喷流 | astrophysical(relativistic) jet |
| 恒星级质量黑洞 | stellar black hole |
| 超大质量黑洞 | supermassive black hole |
| 伽马射线暴 | gamma-ray burst, GRB |
| 引力波 | gravitational wave |
| 旋臂 | spiral arm |
| 核球 | bulge |
| 星系盘 | galactic disk |
| 星系晕 | galactic halo |
| 尘埃带 | dust lane |
| 宇宙射线 | cosmic ray |
| 密度波 | density wave |
| 潮汐瓦解 | tidal disruption |
| 椭圆星系 | elliptical galaxy |
| 旋涡星系 | spiral galaxy |
| 棒旋星系 | barred spiral galaxy |
| 不规则星系 | irregular galaxy |
| 矮星系 | dwarf galaxy |
| 河外星系 | extragalactic system |
| 暗物质 | dark matter |
| 标准烛光 | standard candle |
| 距离阶梯 | distance ladder |
| 类星体 | quasar |
| 引力红移 | gravitational redshift |
| 宇宙学红移 | cosmological redshift |
| 活动星系核 | active galactic nucleus, AGN |
| 射电噪的 | radio-loud |
| 射电宁静的 | radio-quiet |
| 射电星系 | radio galaxy |
| 耀变体 | blazar |
| 辐射压 | radiation pressure |
| 尘埃环 | obscuring torus |
| 宇宙学原理 | cosmological principle |
| (宇宙是)均匀的 | homogeneous |
| (宇宙是)各向同性的 | isotropic |
| 退行速度 | recessional velocity |
| 本动速度 | peculiar velocity |
| 回溯时间 | look-back time |
| 宇宙大爆炸 | the Big Bang |
| 宇宙尺度因子 | scale factor |
| 宇宙微波背景辐射 | cosmic microwave background radiation, CMB |
| 复合(光子退耦) | recombination |
| 星系群 | galaxy group |
| 星系团 | galaxy cluster |
| 超星系团 | supercluster |
| 巨洞 | void |
| 大尺度结构 | large-scale structure |
| 等级式成团 | hierarchical clustering |
| 黑暗时代 | the Dark Ages |
| 再电离 | reionization |
| 量子涨落 | quantum fluctuation |
| 临界密度 | critical density |
| 宇宙学常数 | the cosmological constant |
| 暗能量 | dark energy |
| 大挤压 | the Big Crunch |
| 大撕裂 | the Big Rip |
| 平直宇宙 | flat universe |
| 暴涨 | inflation |
| 多重宇宙 | multiverse |
天体
| 中文 | 英文 |
|---|---|
| 太阳系 | the Solar System |
| 银河系 | the Milky Way |
| 本星系群 | the Local Group of Galaxies |
| 本(室女座)超星系群 | the Local(Virgo) Supercluster |
| 拉尼亚凯亚超星系团 | the Laniakea Supercluster |
| 仙女座星系 | the Andromeda Galaxy |
| 三角座星系 | the Triangulum Galaxy |
| 大/小麦哲伦星云 | the Large/Small Magellanic Cloud |
| 北极星 | Polaris |
| 天狼星 | Sirius |
| 比邻星 | Proxima Centauri |
| 昴星团 | the Pleiades |
| 蟹状星云 | the Crab Nebula |
人名
| 中文 | 英文 | 贡献 | 诺贝尔奖 |
|---|---|---|---|
| 托勒密 | Ptolemy | 地心说(150 年《天文学大成》) | |
| 哥白尼 | Copernicus | 日心说(1543 年《天体运行论》) | |
| 第谷 | Tycho | 望远镜之前最好的天文仪器和观测 | |
| 开普勒 | Kepler | 观测、开普勒三定律(1619 年《世界的和谐》) | |
| 伽利略 | Galileo | 第一位使用望远镜,彻底否定地心说,发现银河由众多恒星组成 | |
| 牛顿 | Newton | 第一台反射式望远镜、物理(1687 年《自然哲学的数学原理》) | |
| 爱因斯坦 | Einstein | 相对论等 | |
| 根策尔、盖兹 | Genzel, Ghez | 发现银河系中心的黑洞 | 2020 |
| 韦斯、巴里什、索恩 | Weiss, Barish, Thorne | LIGO 探测装置(探测引力波) | 2017 |
| 麦克斯韦 | Maxwell | 电磁场理论(1873 年《论电和磁》) | |
| 普朗克 | Planck | 黑体辐射谱、量子力学创始人之一 | 1918 |
| 韦恩 | Wien | 位移定律 | |
| 斯特藩、玻尔兹曼 | Stefan, Boltzmann | 斯特藩—玻尔兹曼定律 | |
| 玻尔 | Bohr | 原子模型 | 1922 |
| 巴尔末 | Balmer | 巴尔末线系 | |
| 莱曼 | Lyman | 莱曼线系 | |
| 多普勒 | Doppler | 多普勒效应 | |
| 卡塞格林 | Cassegrain | 反射式望远镜 | |
| 艾里 | Airy | 艾里斑 | |
| 瑞利 | Rayleigh | 瑞利散射、判据 | |
| 康德 | Kant | 首先提出太阳系形成的星云假说、认为旋涡星云是“岛宇宙” | |
| 拉普拉斯 | Laplace | 提供星云假说的定量化版本 | |
| 马约尔、奎洛兹 | Mayor, Queloz | 发现第一颗系外行星 | 2019 |
| 贝特 | Bethe | 恒星能源及核反应 | 1967 |
| 戴维斯、小柴昌俊 | Davis, Koshiba | 对天体物理学,特别是对探测宇宙中微子的开拓性贡献 | 2022 |
| 麦克唐纳、梶田隆章 | McDonald, Kajita | 发现了中微子振荡,证实了中微子有质量 | 2015 |
| 赫茨普龙 | Hertzsprung | 赫—罗图 | |
| 罗素 | Russell | 赫—罗图 | |
| 林忠四郎 | Hayashi | 恒星形成模型和前主序列演化模型 | |
| 赫比格、阿罗 | Herbig, Haro | HH 天体 | |
| 洛希 | Roche | 洛希极限、洛希瓣 | |
| 钱德拉塞卡 | Chandrasekhar | 钱德拉塞卡极限 | 1983 |
| 休伊什 | Hewish | 发现第一颗脉冲星 | 1974 |
| 泰勒、赫尔斯 | Taylor, Hulse | 发现第一颗双星射电脉冲星 | 1993 |
| 洛里默 | Lorimer | 发现首例快速射电暴 | |
| 史瓦西 | Schwarzschild | 史瓦西度规与史瓦西半径 | |
| 霍金 | Hawking | 黑洞辐射 | |
| 林家翘 | 密度波理论 | ||
| 梅西耶 | Messier | 梅西耶星表 | |
| 赫歇尔 | Herschel | 银河系结构、NGC、发现天王星,并发现天王星的轨道预言和实际观测不一致 | |
| 沙普利 | Shapley | 发现球状星团三维分布、太阳系不是银河系的中心 | |
| 哈勃 | Hubble | 哈勃分类、哈勃定律 | |
| 施密特 | Schmidt | 首次发现类星体 | |
| 塞弗特 | Seyfert | 赛弗特星系 | |
| 爱丁顿 | Eddington | 爱丁顿光度 | |
| 弗里德曼 | Friedmann | 弗里德曼宇宙模型 | |
| 勒梅特 | Lemaître | 宇宙膨胀模型 | |
| 伽莫夫 | Gamow | αβγ 论文 | |
| 皮布尔斯 | Peebles | 对于物理宇宙学方面的理论发现 | 2019 |
| 彭齐亚斯、威尔逊 | Penzias, Wilson | 发现宇宙微波背景辐射 | 1978 |
| 马瑟、斯穆特 | Mather, Smoot | 发现了宇宙微波背景辐射的黑体谱形式和各项异性 | 2006 |
| 兹威基 | Zwicky | 星系团的暗物质 | |
| 鲁宾 | Rubin | 星系的暗物质 | |
| 珀尔马特、施密特、里斯 | Perlmutter, Schmidt, Riess | 通过观测遥远的超新星发现宇宙正在加速膨胀 | 2011 |
| 古斯 | Guth | 提出大爆炸后暴胀期 |
望远镜
| 中文 | 缩写 | 贡献 |
|---|---|---|
| 韦布太空望远镜 | JWST | 首张“全彩”红外照片、早期星系、“长城”、最遥远的黑洞合并、创世之柱(红外) |
| 胡克望远镜 | Hooker | 为哈勃定律、赫—罗图提供数据 |
| 哈勃太空望远镜 | HST | 深空、创世之柱(可见光) |
| 钱德拉 X 射线太空望远镜 | CXO | 蟹状星云 X 射线图像、一些黑洞的 X 射线图像 |
| 事件视界望远镜 | EHT | M87* 黑洞、Sgr A* 黑洞 |
